
 ��Բ$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1��a��b��0���ľ������ĵ��ҳ�Ϊ��Բ��һ��ֱ����ƽ���ڸ�ֱ���������ҵ��е�Ĺ켣Ϊһ���߶Σ���Ϊ��ֱ���Ĺ���ֱ������֪��Բ�ķ���Ϊ$\frac{x^2}{4}$+y2=1��
��Բ$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1��a��b��0���ľ������ĵ��ҳ�Ϊ��Բ��һ��ֱ����ƽ���ڸ�ֱ���������ҵ��е�Ĺ켣Ϊһ���߶Σ���Ϊ��ֱ���Ĺ���ֱ������֪��Բ�ķ���Ϊ$\frac{x^2}{4}$+y2=1������ ��1����б��Ϊ$\frac{1}{3}$����ֱ��ƽ�е��ҵĶ˵�����ֱ�Ϊ��x1��y1������x2��y2���������е�Ϊ��x��y��������ƽ������������ֱ���Ĺ���ֱ�����ڵ�ֱ�߷��̣�
��2����Բ����������ֱ��ΪAB��CD�����ǵ�б�ʷֱ�Ϊk1��k2������ABƽ�е��ҵĶ˵�����ֱ�Ϊ��x1��y1������x2��y2������ʾ��б�ʣ�������������Բ���̣�����ƽ������б�ʹ�ϵ��Ȼ�����A��B��C��D���꣬���C��ֱ��AB�ľ���Ϊd���������ı���ʽ����������ı���ACBD������Ƿ��Ƕ�ֵ��
��� �⣺��1����б��Ϊ$\frac{1}{3}$����ֱ��ƽ�е��ҵĶ˵�����ֱ�Ϊ��x1��y1������x2��y2����
�����е�Ϊ��x��y��������$\frac{x_1^2}{4}+y_1^2=1$��$\frac{x_2^2}{4}+y_2^2=1$��
����ã�$\frac{{��{x_1}-{x_2}����{x_2}+{x_2}��}}{4}+��{y_1}-{y_2}����{y_1}+{y_2}��=0$��
����$x=\frac{{{x_1}+{x_2}}}{2}$��$y=\frac{{{y_1}+{y_2}}}{2}$����$\frac{{{y_1}-{y_2}}}{{{x_1}-{x_2}}}=\frac{1}{3}$�����Եã�3x+4y=0��
�ʸ�ֱ���Ĺ���ֱ�����ڵ�ֱ�߷���Ϊ3x+4y=0��
��2����Բ����������ֱ��ΪAB��CD�����ǵ�б�ʷֱ�Ϊk1��k2��
�ı���ACBD��ȻΪƽ���ı��Σ�
����ABƽ�е��ҵĶ˵�����ֱ�Ϊ��x1��y1������x2��y2����
��${k_1}=\frac{{{y_1}-{y_2}}}{{{x_1}-{x_2}}}$��${k_2}=\frac{{{y_1}+{y_2}}}{{{x_1}+{x_2}}}$����$\frac{x_1^2}{4}+y_1^2=1$��$\frac{x_2^2}{4}+y_2^2=1$��$\frac{{��{x_1}-{x_2}����{x_2}+{x_2}��}}{4}+��{y_1}-{y_2}����{y_1}+{y_2}��=0$��
��${k_1}{k_2}=\frac{y_1^2-y_2^2}{x_1^2-x_2^2}=-\frac{1}{4}$��
��$\left\{\begin{array}{l}y={k_1}x\\ \frac{x^2}{4}+{y^2}=1\end{array}\right.$��A��B������ֱ�Ϊ$��\frac{2}{{\sqrt{1+4k_1^2}}}��\frac{{2{k_1}}}{{\sqrt{1+4k_1^2}}}��$��$��-\frac{2}{{\sqrt{1+4k_1^2}}}��-\frac{{2{k_1}}}{{\sqrt{1+4k_1^2}}}��$
��$|{AB}|=\frac{4}{{\sqrt{1+4k_1^2}}}\sqrt{1+k_1^2}$��
ͬ��C��D������ֱ�Ϊ$��\frac{2}{{\sqrt{1+4k_2^2}}}��\frac{{2{k_2}}}{{\sqrt{1+4k_2^2}}}��$��$��-\frac{2}{{\sqrt{1+4k_2^2}}}��-\frac{{2{k_2}}}{{\sqrt{1+4k_2^2}}}��$
���C��ֱ��AB�ľ���Ϊd���ı���ACBD�����ΪS��
���ԣ�$d=\frac{{|{\frac{{2{k_1}}}{{\sqrt{1+4k_2^2}}}-\frac{{2{k_2}}}{{\sqrt{1+4k_2^2}}}}|}}{{\sqrt{1+k_1^2}}}=\frac{{2|{{k_1}-{k_2}}|}}{{\sqrt{1+k_1^2}\sqrt{1+4k_2^2}}}$��
��$S=d|AB|=\frac{2|{k}_{1}-{k}_{2}|}{\sqrt{1+{{k}_{1}}^{2}}\sqrt{1+4{{k}_{2}}^{2}}}��\frac{4}{\sqrt{1+4{{k}_{1}}^{2}}}•\sqrt{1+{{k}_{1}}^{2}}$
=$\frac{8|{k}_{1}-{k}_{2}|}{\sqrt{1+4{{k}_{1}}^{2}}\sqrt{1+4{{k}_{2}}^{2}}}$
=8$\sqrt{\frac{{{k}_{1}}^{2}+{{k}_{2}}^{2}-2{k}_{1}{k}_{2}}{1+4��{{k}_{1}}^{2}+{{k}_{2}}^{2}��+16{{k}_{1}}^{2}{{k}_{2}}^{2}}}$
=4��
Ϊ��ֵ��
���� ���⿼��ֱ������Բ��λ�ù�ϵ���ۺ�Ӧ�ã�ƽ�����Ӧ�ã��㵽ֱ�ߵľ��빫ʽ���빫ʽ��Ӧ�ã�����������������������������������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
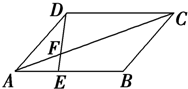
| A�� | 16 cm2 | B�� | 18 cm2 | C�� | 20 cm2 | D�� | 22 cm2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017����������һ�и�����ѧ��9���¿���ѧ���ģ��Ծ��������棩 ���ͣ������
ѡ��4��5������ʽѡ��
��֪����f��x����|2x��a|��a.
��1��������ʽf��x����6�Ľ⼯Ϊ{x|��2��x��3}����ʵ��a��ֵ��
��2���ڣ�1���������£�������ʵ��nʹf��n����m��f����n����������ʵ��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017����������һ�и�����ѧ��9���¿���ѧ�������Ծ��������棩 ���ͣ�ѡ����
�躯��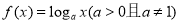 ����
����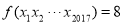 ����
����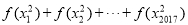 ��ֵ���ڣ� ��
��ֵ���ڣ� ��
A��2loga8 B��16 C��8 D��4
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com