
分析 (Ⅰ)利用l与f (x)图象相切的切点为(1,0),求出导函数f′(x)=$\frac{1}{x}$,得到切线斜率kl=1,求出l方程,利用直线与抛物线联立,判别式为0,求解a即可.
(Ⅱ)记h(x)=f ( x2+1)-g(x)-ln2 化简,然后求出导函数,通过h'(x)<0,h'(x)>0,得到单调区间,求出极值和最值,即可得到不等式f ( x2+1)≤ln2+g(x) 的解集.
解答 解:(Ⅰ)依题意,l与f (x)图象相切的切点为(1,0),函数f (x)=ln x,可得f′(x)=$\frac{1}{x}$,
∴kl=1,从而l:y=x-1…3’;
又$\left\{\begin{array}{l}y=\frac{1}{2}{x^2}+a\\ y=x-1\end{array}\right.⇒$x2-2x+2a+2=0,判别式△=4-8a-8=0 $⇒a=-\frac{1}{2}$…6’.
(Ⅱ)记h(x)=f ( x2+1)-g(x)-ln2…7’,
则h(x)=ln ( x2+1)-$\frac{1}{2}{x^2}+\frac{1}{2}$-ln2 (x∈R)…8’,
$h'(x)=\frac{2x}{{{x^2}+1}}-x=\frac{{x-{x^3}}}{{{x^2}+1}}$=$\frac{-(x+1)x(x-1)}{{{x^2}+1}}$,
令h'(x)<0,得(x+1)x(x-1)>0,即-1<x<0或x>1;
令h'(x)>0,得(x+1)x(x-1)<0,即x<-1或0<x<1,
可见x=-1及x=1时偶函数h(x)取得极大值…10’,也是最大值,hmax(x)=h(±1)=0,
∴h(x)≤0在R上恒成立,即不等式f ( x2+1)≤ln2+g(x) 的解集为R…12’.
点评 本题考查函数与导数的综合应用,函数的最值以及切线方程的求法,考查转化思想以及计算能力.


科目:高中数学 来源: 题型:解答题
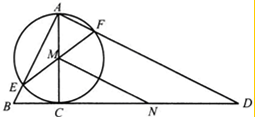 AC是圆O的直径,BD是圆O在点C处的切线,AB、AD分别与圆O相交于E,F,EF与AC相交于M,N是CD中点,AC=4,BC=2,CD=8
AC是圆O的直径,BD是圆O在点C处的切线,AB、AD分别与圆O相交于E,F,EF与AC相交于M,N是CD中点,AC=4,BC=2,CD=8查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
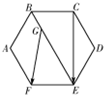 已知边长为2的正六边形ABCDEF中,连接BE、CE,点G是线段BE上靠近B的四等分点,连接GF,则$\overrightarrow{GF}$•$\overrightarrow{CE}$=( )
已知边长为2的正六边形ABCDEF中,连接BE、CE,点G是线段BE上靠近B的四等分点,连接GF,则$\overrightarrow{GF}$•$\overrightarrow{CE}$=( )| A. | -6 | B. | -9 | C. | 6 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的经过中心的弦称为椭圆的一条直径,平行于该直径的所有弦的中点的轨迹为一条线段,称为该直径的共轭直径,已知椭圆的方程为$\frac{x^2}{4}$+y2=1.
椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的经过中心的弦称为椭圆的一条直径,平行于该直径的所有弦的中点的轨迹为一条线段,称为该直径的共轭直径,已知椭圆的方程为$\frac{x^2}{4}$+y2=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届甘肃会宁县一中高三上学期9月月考数学(文)试卷(解析版) 题型:解答题
已知函数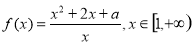 .
.
(1)当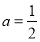 时,求函数
时,求函数 的最小值;
的最小值;
(2)若对任意x∈[1,+∞),f(x)>0恒成立,试求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2017届甘肃会宁县一中高三上学期9月月考数学(理)试卷(解析版) 题型:选择题
下列选项中,说法正确的是( )
A.命题“?x0∈R,x-x0≤0”的否定是“?x0∈R,x-x0>0”
B.命题“p∨q为真”是命题“p∧q为真”的充分不必要条件
C.命题“若am2≤bm2,则a≤b”是假命题
D.命题“在△ABC中,若sin A<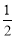 ,则A<
,则A<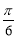 ”的逆否命题为真命题
”的逆否命题为真命题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com