
分析 求得抛物线的焦点,设A($\frac{{{y}_{1}}^{2}}{4}$,y1),B($\frac{{{y}_{2}}^{2}}{4}$,y2),C($\frac{{{y}_{3}}^{2}}{4}$,y3),由重心坐标公式,可得$\frac{1}{3}$•$\frac{{{y}_{1}}^{2}+{{y}_{2}}^{2}+{{y}_{3}}^{2}}{4}$=1,$\frac{{y}_{1}+{y}_{2}+{y}_{3}}{3}$=0,消去y3,可得y12+y22+y1y2=6,由基本不等式可得0≤y1y2≤2.运用向量的数量积求得三角形的面积公式,运用重心的性质,可得△FAB、△FBC、△FCA的面积相等,且为△ABC的面积的$\frac{1}{3}$.求出S△FAB的表达式,运用换元法和导数,判断单调性,可得最大值.
解答 解:抛物线y2=4x的焦点为(1,0),
设A($\frac{{{y}_{1}}^{2}}{4}$,y1),B($\frac{{{y}_{2}}^{2}}{4}$,y2),C($\frac{{{y}_{3}}^{2}}{4}$,y3),
可得△ABC的重心为($\frac{1}{3}$•$\frac{{{y}_{1}}^{2}+{{y}_{2}}^{2}+{{y}_{3}}^{2}}{4}$,$\frac{{y}_{1}+{y}_{2}+{y}_{3}}{3}$),
由题意可得$\frac{1}{3}$•$\frac{{{y}_{1}}^{2}+{{y}_{2}}^{2}+{{y}_{3}}^{2}}{4}$=1,$\frac{{y}_{1}+{y}_{2}+{y}_{3}}{3}$=0,
将y3=-(y1+y2),代入第一式可得y12+y22+y1y2=6,
由y12+y22≥2y1y2,可得y1y2≤2.
可设0≤y1y2≤2.
由F为△ABC的重心,可得△FAB、△FBC、△FCA的面积相等,
且为△ABC的面积的$\frac{1}{3}$.
由$\overrightarrow{FA}$=($\frac{{{y}_{1}}^{2}}{4}$-1,y1),$\overrightarrow{FB}$=($\frac{{{y}_{2}}^{2}}{4}$-1,y2),
可得S△FAB=$\frac{1}{2}$|$\overrightarrow{FA}$|•|$\overrightarrow{FB}$|sin<$\overrightarrow{FA}$,$\overrightarrow{FB}$>=$\frac{1}{2}$$\sqrt{|\overrightarrow{FA}{|}^{2}•|\overrightarrow{FB}{|}^{2}-(\overrightarrow{FA}•\overrightarrow{FB})^{2}}$
=$\frac{1}{2}$$\sqrt{(\frac{{{y}_{1}}^{2}}{4}+1)^{2}(\frac{{{y}_{2}}^{2}}{4}+1)^{2}-({y}_{1}{y}_{2}+(\frac{{{y}_{1}}^{2}}{4}-1)(\frac{{{y}_{2}}^{2}}{4}-1))^{2}}$
=$\frac{1}{2}$|(y1-y2)(1+$\frac{{y}_{1}{y}_{2}}{4}$)|,
由y12+y22+y1y2=6,可得(y1-y2)2=6-3y1y2,
可令t=y1y2,可得z=(6-3t)(1+$\frac{t}{4}$)2,
导数z′=-3(1+$\frac{t}{4}$)2+$\frac{1}{2}$(6-3t)(1+$\frac{t}{4}$)=-$\frac{9t}{4}$(1+$\frac{t}{4}$),
由t∈[0,2],z′≤0,即函数z递减,可得t=0时,取得最大值6.
即有S△FAB的最大值为$\frac{\sqrt{6}}{2}$,
可得△ABC面积的最大值为$\frac{3\sqrt{6}}{2}$,
此时可得A(0,0),B($\frac{3}{2}$,$\sqrt{6}$),C($\frac{3}{2}$,-$\sqrt{6}$).
点评 本题考查三角形的面积的最值的求法,注意运用重心的坐标公式和重心的性质:连接重心和三个顶点的三角形的面积相等且为原三角形的面积的$\frac{1}{3}$,考查化简整理的运算能力,运用向量法是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 210 | B. | 420 | C. | 630 | D. | 840 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 0 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a为任意实数 | B. | a=f′(3) | C. | a>f′(3) | D. | a<f′(3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
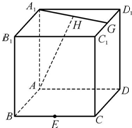 如图,在棱长为1的正方体ABCD-A1B1C1D1中,E是BC的中点,F是棱CD上的动点,G为C1D1的中点,H为A1G的中点.
如图,在棱长为1的正方体ABCD-A1B1C1D1中,E是BC的中点,F是棱CD上的动点,G为C1D1的中点,H为A1G的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com