
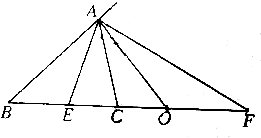
 如图所示,AE、AF分别为△ABC的内、外角平分线,O为EF的中点.
如图所示,AE、AF分别为△ABC的内、外角平分线,O为EF的中点. 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | a为任意实数 | B. | a=f′(3) | C. | a>f′(3) | D. | a<f′(3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 成功(人) | 失败(人) | 合计 | |
| 20~30(岁) | 20 | 40 | 60 |
| 30~40(岁) | 50 | ||
| 合计 | 70 |
| P(K2≥k) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2017届甘肃兰州一中高三9月月考数学(文)试卷(解析版) 题型:选择题
已知直线l:x+ay-1=0(a R)是圆C:
R)是圆C: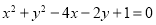 的对称轴.过点A(-4,a)作圆C的一条切线,切点为B,则|AB|= ( )
的对称轴.过点A(-4,a)作圆C的一条切线,切点为B,则|AB|= ( )
A.2 B. C.6 D.
C.6 D.
查看答案和解析>>
科目:高中数学 来源:2017届甘肃会宁县一中高三上学期9月月考数学(理)试卷(解析版) 题型:解答题
已知函数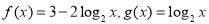 .
.
(1)当x∈[1,4]时,求函数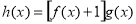 的值域;
的值域;
(2)如果对任意的x∈[1,4],不等式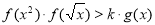 恒成立,求实数k的取值范围
恒成立,求实数k的取值范围
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com