
分析 根据椭圆的标准方程求出c,利用双曲线的离心率建立方程求出a,b,即可求出双曲线的渐近线方程.
解答 解:∵椭圆的标准方程为$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1,
∴椭圆中的a1=5,b1=3,则c=4,
∵双曲线的焦点与椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1的焦点相同,
∴双曲线中c=4,
∵双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的离心率为2,
∴e=$\frac{c}{a}$=$\frac{4}{a}$=2,则a=2.
在双曲线中b=$\sqrt{{c}^{2}-{a}^{2}}$=$\sqrt{16-4}$=$\sqrt{12}$=2$\sqrt{3}$,
则双曲线的渐近线方程为y=±$\frac{b}{a}$x=±$\frac{2\sqrt{3}}{2}$x=±$\sqrt{3}$x,
故答案为:y=±$\sqrt{3}$x.
点评 本题主要考查双曲线渐近线的求解,根据椭圆和双曲线的关系建立方程求出a,b,c是解决本题的关键.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:高中数学 来源: 题型:解答题
| 男 | 女 | 总计 | |
| 需要帮助 | 40 | m | 70 |
| 不需要帮助 | n | 270 | s |
| 总计 | 200 | t | 500 |
| y1 | y2 | 总计 | |
| x1 | a | b | a+b |
| x2 | c | d | c+d |
| 总计 | a+c | b+d | a+b+c+d |
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,平行四边形ABCD中,AE:EB=1:2.
如图,平行四边形ABCD中,AE:EB=1:2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
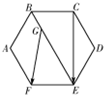 已知边长为2的正六边形ABCDEF中,连接BE、CE,点G是线段BE上靠近B的四等分点,连接GF,则$\overrightarrow{GF}$•$\overrightarrow{CE}$=( )
已知边长为2的正六边形ABCDEF中,连接BE、CE,点G是线段BE上靠近B的四等分点,连接GF,则$\overrightarrow{GF}$•$\overrightarrow{CE}$=( )| A. | -6 | B. | -9 | C. | 6 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
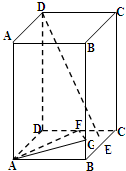 如图,在正四棱柱ABCD-A1B1C1D1中,侧棱AA1=2AB,E是BC中点,F是CD中点,
如图,在正四棱柱ABCD-A1B1C1D1中,侧棱AA1=2AB,E是BC中点,F是CD中点,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届甘肃会宁县一中高三上学期9月月考数学(理)试卷(解析版) 题型:选择题
已知定义在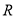 上的奇函数
上的奇函数 满足
满足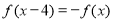 ,且在区间[0,2]上是增函数,则( )
,且在区间[0,2]上是增函数,则( )
A.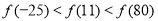 B.
B.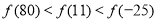
C.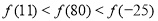 D.
D.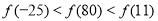
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com