
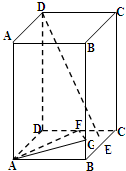
 如图,在正四棱柱ABCD-A1B1C1D1中,侧棱AA1=2AB,E是BC中点,F是CD中点,
如图,在正四棱柱ABCD-A1B1C1D1中,侧棱AA1=2AB,E是BC中点,F是CD中点,分析 (Ⅰ)设正四棱柱底面边长为2,求出侧棱长,分别以DA、DC、DD1方向为x、y、z轴,建立空间直角坐标系,求出相关点的坐标,设G(2,2,m),利用$\overrightarrow{{D_1}E}•\overrightarrow{AG}=0$且$\overrightarrow{{D_1}E}•\overrightarrow{FG}=0$,求出m值,即可得到结果.
(Ⅱ)求出面AFG的一个法向量,面AFE的一个法向量,利用空间向量的数量积求解G-AF-E的二面角的余弦值.
解答 解:(Ⅰ)设正四棱柱底面边长为2,则侧棱长为4…1’
分别以DA、DC、DD1方向为x、y、z轴
建立空间直角坐标系,则D(0,0,0),A(2,0,0),B(2,2,0),C(0,2,0),
E(1,2,0),F(0,1,0),D1(0,0,4),
设G(2,2,m)…3’
则$\overrightarrow{{D_1}E}=(1,2,-4)$,$\overrightarrow{AG}=(0,2,m)$,$\overrightarrow{FG}=(2,1,m)$,
当$\overrightarrow{{D_1}E}⊥\overrightarrow{AG}$且$\overrightarrow{{D_1}E}⊥\overrightarrow{FG}$时,D1E⊥平面AFG,
此时$\overrightarrow{{D_1}E}•\overrightarrow{AG}=0$且$\overrightarrow{{D_1}E}•\overrightarrow{FG}=0$,
即$\left\{\begin{array}{l}1×0+2×2-4m=0\\ 1×2+2×1-4m=0\end{array}\right.⇒m=1$,
∴BG=1时满足题意…6’.
(Ⅱ)依题意,$\overrightarrow{{D_1}E}=(1,2,-4)$就是面AFG的一个法向量,…7’
而面AFE的一个法向量是$\overrightarrow{D{D_1}}=(0,0,4)$,…8’
∴$cos<\overrightarrow{{D_1}E},\overrightarrow{D{D_1}}>=\frac{{\overrightarrow{{D_1}E}•\overrightarrow{D{D_1}}}}{{|{\overrightarrow{{D_1}E}}|•|{\overrightarrow{D{D_1}}}|}}=\frac{-16}{{\sqrt{21}•4}}=-\frac{{4\sqrt{21}}}{21}$,…10’
∵G-AF-E是锐二面角,记其大小为θ,则$cosθ=\frac{{4\sqrt{21}}}{21}$…12’.
点评 本题考查空间向量的应用,直线与平面垂直,二面角的求法,数量积的应用,考查计算能力.


科目:高中数学 来源: 题型:解答题
 如图,△ABC为⊙O的内接三角形,D,E分别为BC,AB的中点,直线DE交圆O于F,G,且直线DE与过A点的切线交于点P,DF=1,DE=2,PE=3.
如图,△ABC为⊙O的内接三角形,D,E分别为BC,AB的中点,直线DE交圆O于F,G,且直线DE与过A点的切线交于点P,DF=1,DE=2,PE=3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2017届甘肃兰州一中高三9月月考数学(文)试卷(解析版) 题型:选择题
已知直线l:x+ay-1=0(a R)是圆C:
R)是圆C: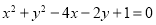 的对称轴.过点A(-4,a)作圆C的一条切线,切点为B,则|AB|= ( )
的对称轴.过点A(-4,a)作圆C的一条切线,切点为B,则|AB|= ( )
A.2 B. C.6 D.
C.6 D.
查看答案和解析>>
科目:高中数学 来源:2017届甘肃会宁县一中高三上学期9月月考数学(文)试卷(解析版) 题型:解答题
已知函数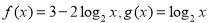 .
.
(1)当x∈[1,4]时,求函数 的值域;
的值域;
(2)如果对任意的x∈[1,4],不等式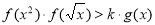 恒成立,求实数k的取值范围
恒成立,求实数k的取值范围
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com