
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据等比数列的前n项和公式先进行化简,结合二项展开式的应用进行求解即可.
解答 解:2+22+23…+25n-1+a=$\frac{2(1-{2}^{5n-1})}{1-2}$+a=25n-2+a=32n-2+a=(31+1)n-2+a
=31n+C${\;}_{n}^{1}$•31n-1+C${\;}_{n}^{2}$•31n-2+…+C${\;}_{n}^{n-1}$•31+1-2+a
=31(31n-1+C${\;}_{n}^{1}$•31n-2+C${\;}_{n}^{2}$•31n-2+…+C${\;}_{n}^{n-1}$)+a-1,
若2+22+23…+25n-1+a被31除所得的余数为3,
则a-1=3,即a=4,
故选:D.
点评 本题主要考查二项展开式的应用,根据等比数列的前n项和公式先进行化简是解决本题的关键.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 有40名高校应届毕业生参加某招工单位应聘,其中甲组20人学历为硕士研究生,乙组20人学历是本科,他们首先参加笔试,统计考试成绩得到的茎叶图如图(满分100分),如果成绩在86分以上(含86分)才可以进入面试阶段
有40名高校应届毕业生参加某招工单位应聘,其中甲组20人学历为硕士研究生,乙组20人学历是本科,他们首先参加笔试,统计考试成绩得到的茎叶图如图(满分100分),如果成绩在86分以上(含86分)才可以进入面试阶段| 本科生 | 研究生 | 合计 | |
| 能参加面试 | |||
| 不能参加面试 | |||
| 合计 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6,635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
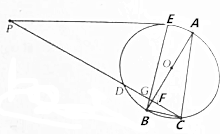 如图所示,已知圆O的一条直径为AB,PE是圆O的一条切线,E为切点,PC是圆O的一条割线,且交圆O于C,D两点,AB交PC于F,BE交PC于G,△AFC∽△ACB.
如图所示,已知圆O的一条直径为AB,PE是圆O的一条切线,E为切点,PC是圆O的一条割线,且交圆O于C,D两点,AB交PC于F,BE交PC于G,△AFC∽△ACB.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 女 | 男 | 总计 | |
| 喜欢 | 40 | 20 | 60 |
| 不喜欢 | 20 | 30 | 50 |
| 总计 | 60 | 50 | 110 |
| (K2≥k) | 0.100 | 0.010 | 0.001 |
| k | 2.706 | 6.635 | 10.828 |
| A. | 有99%以上的把握认为“喜欢该电视剧与性别无关” | |
| B. | 有99%以上的把握认为“喜欢该电视剧与性别有关” | |
| C. | 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关” | |
| D. | 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关” |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
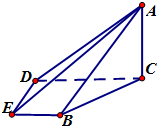 如图,在四棱锥A-BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,AC=$\sqrt{2}$.
如图,在四棱锥A-BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,AC=$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com