
 有40名高校应届毕业生参加某招工单位应聘,其中甲组20人学历为硕士研究生,乙组20人学历是本科,他们首先参加笔试,统计考试成绩得到的茎叶图如图(满分100分),如果成绩在86分以上(含86分)才可以进入面试阶段
有40名高校应届毕业生参加某招工单位应聘,其中甲组20人学历为硕士研究生,乙组20人学历是本科,他们首先参加笔试,统计考试成绩得到的茎叶图如图(满分100分),如果成绩在86分以上(含86分)才可以进入面试阶段| 本科生 | 研究生 | 合计 | |
| 能参加面试 | |||
| 不能参加面试 | |||
| 合计 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6,635 | 7.879 | 10.828 |
分析 (1)由茎叶图得出甲组90(分)与95(分)以上的同学数,用列举法求出基本事件数,计算对应的概率值;
(2)填写列联表,计算观测值,对照临界值表得出结论.
解答 解:(1)甲组90(分)以上的同学数为5人,其中有2名同学分数超95(分),可记为A、B、c、d、e,
从这5人中任取2名,基本事件是AB、Ac、Ad、Ae、Bc、Bd、Be、cd、ce、de共有10种不同取法,
若不含这两名同学,有cd、ce、de共3种不同取法,
因而由古典概型与对立事件概率计算公式得概率
$P=1-\frac{3}{10}=\frac{7}{10}$;
(2)2×2列联表为
| 本科生 | 研究生 | 合计 | |
| 能参加面试 | 3 | 9 | 12 |
| 不能参加面试 | 17 | 11 | 28 |
| 合计 | 20 | 20 | 40 |
点评 本题考查了茎叶图与列举法求古典概型的概率问题,也考查了独立性检验问题,是基础题目.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:高中数学 来源: 题型:解答题
 如图所示,在△ABC中,CD是∠ACB的角平分线,△ADC的外接圆交线段BC于点E,BE=3AD.
如图所示,在△ABC中,CD是∠ACB的角平分线,△ADC的外接圆交线段BC于点E,BE=3AD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
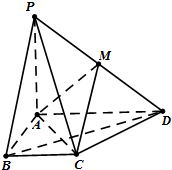 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AB⊥AD,BC=$\frac{2\sqrt{3}}{3}$,AB=1,BD=PA=2,M 为PD的中点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AB⊥AD,BC=$\frac{2\sqrt{3}}{3}$,AB=1,BD=PA=2,M 为PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
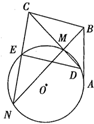 如图,BA与圆O相切,切点为A,割线BN与圆O分别交于点M,N,若BA=BC,连接CM并延长,交圆O于点D,割线CN与圆O的另一个交点为E.
如图,BA与圆O相切,切点为A,割线BN与圆O分别交于点M,N,若BA=BC,连接CM并延长,交圆O于点D,割线CN与圆O的另一个交点为E.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com