
分析 (Ⅰ)由两角和差的正弦公式可得f(x)的解析式,然后利用正弦函数的性质即可求出f(x)在[$0,\frac{π}{2}$]上的最大值和最小值;
(Ⅱ)先求出函数的单调区间,即可求出m的取值范围.
解答 解:(Ⅰ)f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$=cosx•$\sqrt{3}$sinx-$\frac{1}{2}$cos2x=$\frac{\sqrt{3}}{2}$sin2x-$\frac{1}{2}$cos2x=sin(2x-$\frac{π}{6}$),
当x∈[$0,\frac{π}{2}$]时,(2x-$\frac{π}{6}$)∈[-$\frac{π}{6}$,$\frac{5π}{6}$],
由正弦函数y=sinx在[-$\frac{π}{6}$,$\frac{5π}{6}$]的图象可知,
∴f(x)=sin(2x-$\frac{π}{6}$)∈[f(-$\frac{π}{6}$),f($\frac{π}{2}$)]=[-$\frac{1}{2}$,1],
∴f(x)在[$0,\frac{π}{2}$]上的最大值和最小值分别为1,-$\frac{1}{2}$,
(Ⅱ):由$2kπ-\frac{π}{2}≤2x-\frac{π}{6}≤2kπ+\frac{π}{2}$得$kπ-\frac{π}{6}≤x≤kπ+\frac{π}{3}$(k∈z),
f(x)在[-$\frac{π}{6}$,$\frac{π}{3}$]单调递增,
∵f(x)在[-$\frac{π}{6}$,m]上不单调,
∴m>$\frac{π}{3}$
点评 本题考查平面向量的数量积运算,考查了三角函数中的恒等变换应用,考查正弦函数的图象和性质,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | $(2,{e^{\frac{3}{2}}})$ | B. | $(\frac{3}{2},+∞)$ | C. | $(ln2,{e^{\frac{3}{2}}})$ | D. | $(ln2,\frac{3}{2})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,3,4} | B. | {1,4} | C. | {3,4} | D. | {1,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年龄段 | 外国传统节日 | 中国传统节日 | ||
| 获优惠劵的人数 | 占本组人数频率 | 获优惠券的人数 | 占本组人数频率 | |
| [10,20) | 30 | a | 30 | 0.5 |
| [20,30) | 48 | 0.8 | 36 | 0.6 |
| [30,40) | 36 | 0.6 | 48 | 0.8 |
| [40,50) | 20 | 0.5 | 24 | b |
| [50,60] | 4 | 0.2 | 16 | 0.8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
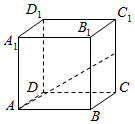 在棱长为1的正方体ABCD-A1B1C1D1中,点F是棱CC1的中点,P是正方体表面上的一点,若D1P⊥AF,则线段D1P长度的取值范围是( )
在棱长为1的正方体ABCD-A1B1C1D1中,点F是棱CC1的中点,P是正方体表面上的一点,若D1P⊥AF,则线段D1P长度的取值范围是( )| A. | (0,$\sqrt{2}$) | B. | (0,$\frac{\sqrt{34}}{4}$] | C. | (0,$\frac{3}{2}$] | D. | (0,$\sqrt{3}$] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com