
分析 (1)先证明数列{$\frac{{a}_{n}}{{2}^{n}}$}是以2为首项,1为公差的等差数列;要证明数列{$\frac{{a}_{n}}{{2}^{n}}$}是等差数列,先根据sn-sn-1=an,用作差法得到an,an-1的关系,再用定义证明,即可得到通项公式;
(2)若不等式2n2-n-3<(5-λ)an对?n∈N*恒成立,求λ的取值范围,用分离参数法,5-λ>$\frac{2n-3}{{2}^{n}}$对?n∈N*恒成立,根据数列的函数特征,即可求出λ的取值范围.
解答 解:(1)∵Sn=2an-2n+1,
∴n=1时,S1=a1=2a1-4,解得a1=4,
当n≥2时,
∴Sn-1=2an-1-2n,
∴Sn-Sn-1=2an-2n+1-2an-1+2n=an,
∴an=2an-1+2n,
∴$\frac{{a}_{n}}{{2}^{n}}$-$\frac{{a}_{n-1}}{{2}^{n-1}}$=$\frac{2{a}_{n-1}+{2}^{n}}{{2}^{n}}$-$\frac{{a}_{n-1}}{{2}^{n-1}}$=$\frac{{a}_{n-1}}{{2}^{n-1}}$+1-$\frac{{a}_{n-1}}{{2}^{n-1}}$=1,
∵$\frac{{a}_{1}}{2}$=$\frac{4}{2}$=2
∴数列{$\frac{{a}_{n}}{{2}^{n}}$}是以2为首项,1为公差的等差数列,
∴$\frac{{a}_{n}}{{2}^{n}}$=2+1×(n-1)=n+1,
∴an=(n+1)2n;
当n=1时,成立.
∴数列{an}的通项公式an=(n+1)2n;
(2)∵不等式2n2-n-3<(5-λ)an对?n∈N*恒成立,
∴2n2-n-3=(n+1)(2n-3)<(5-λ)(n+1)2n对?n∈N*恒成立,
∴5-λ>$\frac{2n-3}{{2}^{n}}$对?n∈N*恒成立,
设bn=$\frac{2n-3}{{2}^{n}}$,
则b1=-$\frac{1}{2}$,b2=$\frac{1}{4}$,b3=$\frac{3}{8}$,b4=$\frac{5}{16}$,
当n≥4时,bn-bn-1=$\frac{2n-3}{{2}^{n}}$-$\frac{2n-5}{{2}^{n-1}}$=$\frac{7-2n}{{2}^{n}}$<0,
∴当n≥3时,数列{bn}为递减数列,
∴当n=3时,数列{bn}有最大值,最大值为$\frac{3}{8}$,
∴5-λ>$\frac{3}{8}$,
∴λ<$\frac{37}{8}$.
点评 本题考查了通项公式与前n项和公式的关系,等差数列的定义的应用.恒成立问题主要利用分离参数法转化为求最值问题解决.


科目:高中数学 来源: 题型:解答题
 在平角坐标系xOy中,椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率$e=\frac{1}{2}$,且过点$(0,\sqrt{3})$,椭圆C的长轴的两端点为A,B,点P为椭圆上异于A,B的动点,定直线x=4与直线PA、PB分别交于M,N两点.
在平角坐标系xOy中,椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率$e=\frac{1}{2}$,且过点$(0,\sqrt{3})$,椭圆C的长轴的两端点为A,B,点P为椭圆上异于A,B的动点,定直线x=4与直线PA、PB分别交于M,N两点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
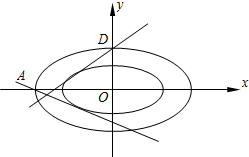 设椭圆E1的长半轴长为a1、短半轴长为b1,椭圆E2的长半轴长为a2、短半轴长为b2,若$\frac{{a}_{1}}{{a}_{2}}$=$\frac{{b}_{1}}{{b}_{2}}$,则我们称椭圆E1与椭圆E2是相似椭圆.已知椭圆E:$\frac{x^2}{2}$+y2=1,其左顶点为A、右顶点为B.
设椭圆E1的长半轴长为a1、短半轴长为b1,椭圆E2的长半轴长为a2、短半轴长为b2,若$\frac{{a}_{1}}{{a}_{2}}$=$\frac{{b}_{1}}{{b}_{2}}$,则我们称椭圆E1与椭圆E2是相似椭圆.已知椭圆E:$\frac{x^2}{2}$+y2=1,其左顶点为A、右顶点为B.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 高一 | 高二 | 总计 | |
| 合格人数 | 70 | x | 150 |
| 不合格人数 | y | 20 | 50 |
| 总计 | 100 | 100 | 200 |
| k0 | 5.024 | 6.635 | 7.879 | 10.828 |
| P(k2≥k0) | 0.025 | 0.010 | 0.005 | 0.001 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
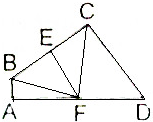 如图所示,四边形ABCD中,AB=1,AD=7,BC=CD=5,∠BAD=∠BCD=90°.
如图所示,四边形ABCD中,AB=1,AD=7,BC=CD=5,∠BAD=∠BCD=90°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
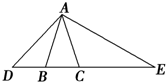 如图,在等腰三角形ABC中,AB=AC,D为CB延长线上一点,E为BC延长线上一点,且满足AB2=DB•CE.
如图,在等腰三角形ABC中,AB=AC,D为CB延长线上一点,E为BC延长线上一点,且满足AB2=DB•CE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com