
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{7}}{3}$ |
分析 取BD中点E,连接AE,CE,则∠PEC是二面角P-BD-C的平面角,由此能求出二面角P-BD-C的正弦值.
解答 解:取BD中点E,连接AE,CE,则∠PEC是二面角P-BD-C的平面角,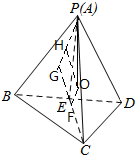
PE=CE=$\frac{3}{2}$,
三棱锥P-BCD的外接球的半径为R,则$\frac{4}{3}×π×{R}^{3}=\frac{7\sqrt{7}π}{6}$,
解得R=$\frac{\sqrt{7}}{2}$,
设△BCD的外接圆的圆心F与球心O的距离为OF=h,
则CF=$\frac{2}{3}CE$=1,
则R2=1+h2,即$\frac{7}{4}=1+{h}^{2}$,解得h=$\frac{\sqrt{3}}{2}$,
过P作PG⊥平面BCD,交CE延长线于G,过O作OH∥CG,交PG于H,
则四边形HGFO是矩形,且HG=OF=h=$\frac{\sqrt{3}}{2}$,PO=R=$\frac{\sqrt{7}}{2}$,
∴$\left\{\begin{array}{l}{E{G}^{2}+(\frac{\sqrt{3}}{2}+PH)^{2}=(\frac{3}{2})^{2}}\\{(\frac{1}{2}+EG)^{2}+P{H}^{2}=(\frac{\sqrt{7}}{2})^{2}}\end{array}\right.$,
解得GE=$\frac{3}{4}$,PH=$\frac{\sqrt{3}}{4}$,∴PG=$\frac{3\sqrt{3}}{4}$,CG=$\frac{9}{4}$,
∴PC=$\sqrt{\frac{27}{16}+\frac{81}{16}}$=$\frac{3\sqrt{3}}{2}$,
∴cos∠PEC=$\frac{\frac{9}{4}+\frac{9}{4}-\frac{27}{4}}{2×\frac{3}{4}×\frac{3}{4}}$=-$\frac{1}{2}$,
∴sin∠PEC=$\sqrt{1-(-\frac{1}{2})^{2}}$=$\frac{\sqrt{3}}{2}$.
∴二面角P-BD-C的正弦值为$\frac{\sqrt{3}}{2}$.
故选:C.
点评 本题考查二面角的正弦值的求法,是中档题,解题时要认真审题,考查学生的计算能力,确定三棱锥P-BCD的外接球的半径是关键.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 等腰三角形 | B. | 直角三角形 | C. | 等腰直角三角形 | D. | 等边三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | -1 | C. | -3 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com