
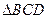 与
与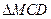 都是边长为2的正三角形,平面
都是边长为2的正三角形,平面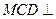 平面
平面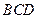 ,
,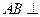 平面BCD,
平面BCD,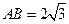 .求点A到平面MBC的距离。
.求点A到平面MBC的距离。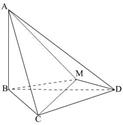
 ,四边形ABCD是矩形.
,四边形ABCD是矩形. ,0),D(0,
,0),D(0, ,0),P(0,0,2),
,0),P(0,0,2), ,PC的中点,
,PC的中点,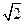 ,0),F(1,
,0),F(1,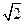 ,1).
,1). =(2,
=(2, ,-2)
,-2) =(-1,
=(-1,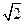 ,1)
,1)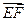 =(1,0,
=(1,0, 1),
1), ·
· =-2+4-2=0,
=-2+4-2=0, ·
·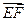 =2+0-2=0,
=2+0-2=0, ⊥
⊥ ,
, ⊥
⊥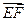 ,
, EF,
EF,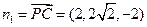 ,
, ,
, . 设平面BEF与平面BAP的夹角为 θ ,
. 设平面BEF与平面BAP的夹角为 θ , ,
, 和
和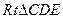 中.
中.  ,F是PC 的中点,
,F是PC 的中点, ,∴
,∴ .
.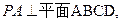 ∴
∴ ,
,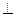 BC
BC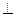 平面BAP,B
平面BAP,B C
C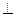 PB,
PB,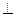 平面BEF,
平面BEF, 中,
中, ∴
∴


科目:高中数学 来源:不详 题型:解答题
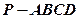 ,
,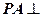 平面
平面 ,
,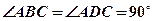 ,
,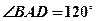 ,
, ,
,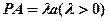 .
.
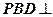 平面
平面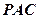 ;
;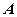 到平面
到平面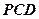 的距离为
的距离为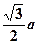 时,求二面角
时,求二面角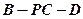 的余弦值;
的余弦值;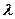 为何值时,点
为何值时,点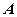 在平面
在平面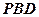 内的射影
内的射影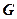 恰好是
恰好是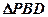 的重心.
的重心.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
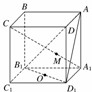
| A.A、M、O三点共线 | B.A、M、O、A1不共面 |
C.A、M、C、O不共面  | D.B、B1、O、M共面 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
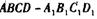 中,DA = DC
中,DA = DC =2,
=2,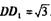 ’E是
’E是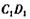 的中点,F是C/:的中点.
的中点,F是C/:的中点.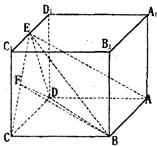
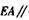 平面BDF
平面BDF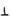 平面
平面查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.直线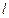 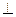 平面 平面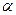 ,平面 ,平面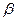 //直线 //直线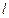 ,则 ,则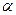 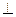 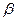 |
B.平面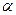 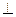 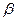 ,直线 ,直线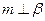 ,则 ,则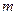 // //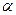 |
C.直线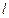 是平面 是平面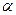 的一条斜线,且 的一条斜线,且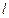 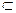 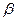 ,则 ,则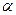 与 与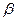 必不垂直 必不垂直 |
| D.一个平面内的两条直线与另一个平面内的两条直线分别平行,则这两个平面平行 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com