
已知函数![]() .,且曲线
.,且曲线![]() 上的点
上的点![]() 处的切线方程为
处的切线方程为![]() .
.
(1)若![]() 在
在![]() 时有极值,求
时有极值,求![]() 的表达式;
的表达式;
(2)若函数![]() 在区间[-2,1]上单调递增,求b的取值范围.
在区间[-2,1]上单调递增,求b的取值范围.
22.解:(1)由![]() 求导数得
求导数得![]() ,………1分
,………1分
过![]() 上点P(1,f(1))处的切线方程为:
上点P(1,f(1))处的切线方程为:![]() ,
,
即![]() ,……………………………………………3分
,……………………………………………3分
而过![]() 上的点
上的点![]() 处的切线方程为
处的切线方程为![]() ,
,
故![]() ,即
,即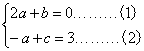 ,
,
因为![]() 在
在![]() 时有极值,
时有极值,
故![]() ………(3)
………(3)
由(1)(2)(3)联立解得![]() ,……………………………………6分
,……………………………………6分
所以![]() .…………………………………………………………7分
.…………………………………………………………7分
(2)![]() 在区间[-2,1]上单调递增,
在区间[-2,1]上单调递增,
又![]() ,由(1)知
,由(1)知![]() ,
,
![]() ,
,
依题意![]() 在[-2,1]上恒成立
在[-2,1]上恒成立![]()
即![]() 在[-2,1]上恒成立.………………………………………………………10分
在[-2,1]上恒成立.………………………………………………………10分
①在![]() 时,
时,![]() ;
;
②在![]() 时,
时,![]() ;
;
③在![]() 时,
时,![]() 则
则![]()
综合上述讨论可知,所求参数b的取值范围是![]() .……………………………………14分
.……………………………………14分


科目:高中数学 来源:2011-2012学年广东省高三第一次模拟考试文科数学 题型:解答题
(本小题满分14分)
已知函数 的图象是曲线C,点
的图象是曲线C,点 是曲线C上的一系列点,
是曲线C上的一系列点,
曲线C在点 处的切线与y轴交于点
处的切线与y轴交于点 。若数列
。若数列 是公差为2的等差
是公差为2的等差
数列,且
(1)分别求出数列 与数列
与数列 的通项公式;
的通项公式;
(2)设O为坐标原点, 表示
表示 的面积,求数列
的面积,求数列 的前项n和
的前项n和
查看答案和解析>>
科目:高中数学 来源:重庆八中2010届高三下学期第二次月考(理) 题型:填空题
已知函数 的图象C上存在一定点P满足:若过点P的直线l与曲线C交于不同于P的两点M(x1,y1)、N(x2,y2),且恒有
的图象C上存在一定点P满足:若过点P的直线l与曲线C交于不同于P的两点M(x1,y1)、N(x2,y2),且恒有 为定值y0,则y0的值为 .
为定值y0,则y0的值为 .
查看答案和解析>>
科目:高中数学 来源:2010年陕西省西安市西工大附中高考数学八模试卷(理科)(解析版) 题型:解答题
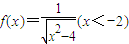 ,点
,点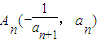 在曲线y=f(x)的图象上(n∈N*),且a1=1.
在曲线y=f(x)的图象上(n∈N*),且a1=1.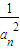 }为等差数列;
}为等差数列;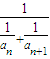 ,记Sn=b1+b2+…+bn,求Sn.
,记Sn=b1+b2+…+bn,求Sn.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com