
【题目】如图,四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,底面
,底面![]() 为梯形,
为梯形,![]() ,
,![]() ,
,![]() ,且
,且![]() 与
与![]() 均为正三角形,
均为正三角形,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 重心.
重心.

(1)求证:![]() 平面
平面![]() ;
;
(2)求三棱锥![]() 的体积.
的体积.
【答案】(Ⅰ)详见解析(Ⅱ)![]()
【解析】
试题分析: (Ⅰ)连接![]() 与
与![]() 交于
交于![]() ,连接
,连接![]() .在梯形
.在梯形![]() 中,根据两平行边的比例,可得
中,根据两平行边的比例,可得![]() 的比值,在
的比值,在![]() 中,由重心的性质,可得
中,由重心的性质,可得![]() 间的比值,两比值相等,则
间的比值,两比值相等,则![]() ,再由线线平行去证明线面平行; (Ⅱ)根据所给条件可证
,再由线线平行去证明线面平行; (Ⅱ)根据所给条件可证![]() ,且求出
,且求出![]() 的长.由
的长.由![]() ,可将所求三棱锥
,可将所求三棱锥![]() 的体转化为求三棱锥
的体转化为求三棱锥![]() 体积,再转化为三棱锥
体积,再转化为三棱锥![]() 体积,又
体积,又![]() ,只需求
,只需求![]() 即可.
即可.
试题解析:(Ⅰ)方法一:连![]() 交
交![]() 于
于![]() ,连接
,连接![]() .
.
由梯形![]() ,
,![]() 且
且![]() ,知
,知![]()
又![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 的重心,∴
的重心,∴![]()
在![]() 中,
中,![]() ,故
,故![]() //
//![]() .
.
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() //平面
//平面![]() .
.
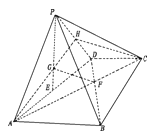
方法二:过![]() 作
作![]() 交
交![]() 于
于![]() ,过
,过![]() 作
作![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,
,
![]()
![]() 为
为![]() 的重心,
的重心,![]() ,
,![]() ,
,
又![]() 为梯形,
为梯形,![]() ,
,![]() ,
,![]()
![]() ,
,![]() ∴
∴![]()
又由所作![]() ,
,![]() 得
得![]() //
//![]() ,
,![]() 为平行四边形.
为平行四边形.
![]() ,
,![]()
![]() 面
面![]()

方法三:过![]() 作
作![]() //
//![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,
,
由![]() 为正三角形,
为正三角形, ![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 重心,
重心,
得![]() ,
,![]()
又由梯形![]() ,
,![]() ,且
,且![]() ,
,
知![]() ,即
,即![]()
∴在![]() 中,
中,![]() //
//![]() ,所以平面
,所以平面![]() //平面
//平面![]()
又![]() 平面
平面![]() ,∴
,∴![]() 面
面![]()
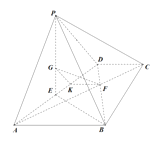
(Ⅱ) 方法一:由平面![]() 平面
平面![]() ,
,![]() 与
与![]() 均为正三角形,
均为正三角形,![]() 为
为![]() 的中点
的中点
∴![]() ,
,![]() ,得
,得![]() 平面
平面![]() ,且
,且![]()
由(Ⅰ)知![]() //平面
//平面![]() ,∴
,∴![]()
又由梯形![]() ,
,![]() ,且
,且![]() ,知
,知![]()
又![]() 为正三角形,得
为正三角形,得![]() ,∴
,∴![]() ,
,
得![]()
∴三棱锥![]() 的体积为
的体积为![]() .
.
方法二: 由平面![]() 平面
平面![]() ,
,![]() 与
与![]() 均为正三角形,
均为正三角形,![]() 为
为![]() 的中点
的中点
∴![]() ,
,![]() ,得
,得![]() 平面
平面![]() ,且
,且![]()
由![]() ,∴
,∴![]()
而又![]() 为正三角形,得
为正三角形,得![]() ,得
,得![]() .
.
∴![]() ,∴三棱锥
,∴三棱锥![]() 的体积为
的体积为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又PA=4,AB=4 ![]() ,∠CDA=120°,点N在线段PB上,且PN=2.
,∠CDA=120°,点N在线段PB上,且PN=2. 
(1)求证:BD⊥PC;
(2)求证:MN∥平面PDC;
(3)求二面角A﹣PC﹣B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,已知3acosA=ccosB+bcosC.
(1)求cosA,sinA的值;
(2)若cosB+cosC= ![]() ,求cosC+
,求cosC+ ![]() sinC的值.
sinC的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某市民众对某项公共政策的态度,在该市随机抽取了![]() 名市民进行调查,做出了他们的月收入(单位:百元,范围:
名市民进行调查,做出了他们的月收入(单位:百元,范围:![]() )的频率分布直方图,同时得到他们月收入情况以及对该项政策赞成的人数统计表:
)的频率分布直方图,同时得到他们月收入情况以及对该项政策赞成的人数统计表:
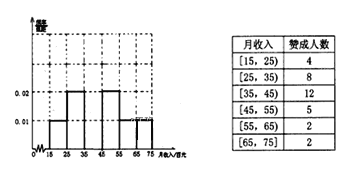
(1)求月收入在![]() 内的频率,并补全这个频率分布直方图,并在图中标出相应纵坐标;
内的频率,并补全这个频率分布直方图,并在图中标出相应纵坐标;
(2)根据频率分布直方图估计这![]() 人的平均月收入;
人的平均月收入;
(3)若从月收入(单位:百元)在![]() 的被调查者中随机选取
的被调查者中随机选取![]() 人,求
人,求![]() 人都不赞成的概率.
人都不赞成的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a∈R,函数f(x)=log2( ![]() +a).
+a).
(1)当a=5时,解不等式f(x)>0;
(2)若关于x的方程f(x)﹣log2[(a﹣4)x+2a﹣5]=0的解集中恰好有一个元素,求a的取值范围.
(3)设a>0,若对任意t∈[ ![]() ,1],函数f(x)在区间[t,t+1]上的最大值与最小值的差不超过1,求a的取值范围.
,1],函数f(x)在区间[t,t+1]上的最大值与最小值的差不超过1,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,已知C= ![]() ,向量
,向量 ![]() =(sinA,1),
=(sinA,1), ![]() =(1,cosB),且
=(1,cosB),且 ![]() .
.
(1)求A的值;
(2)若点D在边BC上,且3 ![]() =
= ![]() ,
, ![]() =
= ![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设p:实数x满足x2﹣4ax+3a2<0,其中a>0; q:实数x满足 ![]() <0.
<0.
(1)若a=1,且p∨q为真,求实数x的取值范围;
(2)若p是q的必要不充分条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学著作《九章算术》有如下问题:“今有人持金出五关,前关二而税一,次关三而税一,次关四而税一,次关五而税一,次关六而税一,并五关所税,适重一斤,问本持金几何”其意思为“今有人持金出五关,第1关收税金 ![]() ,第2关收税金为剩余金的
,第2关收税金为剩余金的 ![]() ,第3关收税金为剩余金的
,第3关收税金为剩余金的 ![]() ,第4关收税金为剩余金的
,第4关收税金为剩余金的 ![]() ,第5关收税金为剩余金的
,第5关收税金为剩余金的 ![]() ,5关所收税金之和,恰好重1斤,问原来持金多少?”若将题中“5关所收税金之和,恰好重1斤,问原来持金多少?”改成假设这个原来持金为x,按此规律通过第8关,则第8关需收税金为x.
,5关所收税金之和,恰好重1斤,问原来持金多少?”若将题中“5关所收税金之和,恰好重1斤,问原来持金多少?”改成假设这个原来持金为x,按此规律通过第8关,则第8关需收税金为x.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com