
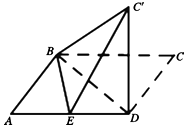
 已知平行四边形ABCD中,AB=6,AD=10,BD=8,E是线段AD的中点.沿BD将△BCD翻折到△BC'D,使得平面BC'D⊥平面ABD.
已知平行四边形ABCD中,AB=6,AD=10,BD=8,E是线段AD的中点.沿BD将△BCD翻折到△BC'D,使得平面BC'D⊥平面ABD.分析 (1)推导出C'D⊥BD,由此能证明C′D⊥平面ABD.
(2)由(1)知C′D⊥平面ABD,且CD⊥BD,以D为原点,DB,CD,DC′所在直线分别为x,y,z轴建立的空间直角坐标系D-xyz,利用同量法能求出二面角D-BE-C'的余弦值.
解答 (本小题满分12分)
解:(1)由题意可知C'D=CD=6,BC'=BC=10,BD=8,
即BC'2=C'D2+BD2,故C'D⊥BD. …(2分)
因为平面BC'D⊥平面ABD,平面BC'D∩平面ABD=BD,
C′D?平面BC′D,所以C′D⊥平面ABD. …(5分)
(2)由(1)知C′D⊥平面ABD,且CD⊥BD,以D为原点,
DB,CD,DC′所在直线分别为x,y,z轴建立如图所示的空间直角坐标系D-xyz,
则d(0,0,0),A(8,6,0),B(8,0,0),C'(0,0,6).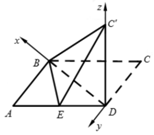
由于E是线段AD的中点,所以E(4,3,0),$\overrightarrow{BD}=(-8,0,0)$.
在平面BEC'中,$\overrightarrow{BE}=(-4,3,0)$,$\overrightarrow{BC'}=(-8,0,6)$,
设平面BEC'的法向量为n=(x,y,z),则$\left\{\begin{array}{l}\overrightarrow{BE}•n=0\\ \overrightarrow{BC'}•n=0\end{array}\right.$,即$\left\{\begin{array}{l}-4x+3y=0\\-8x+6z=0\end{array}\right.$,令x=3,得y=4,z=4,
所以平面BEC'的一个法向量为n=(3,4,4). …(9分)
而平面DBE的一个法向量为$\overrightarrow{DC'}=(0,0,6)$…(10分)
故$cos\left?{n,\overrightarrow{DC'}}\right>=\frac{{n•\overrightarrow{DC'}}}{{|n|•|\overrightarrow{DC'}|}}=\frac{{4\sqrt{41}}}{41}$,
由图易知二面角D-BE-C'的平面角为锐角,所以二面角D-BE-C'的余弦值为$\frac{{4\sqrt{41}}}{41}$. …(12分)
点评 本题考查线面垂直的证明,考查二面角的余弦值的求法,考查推理论证能力、运算求解能力、空间想象能力,考查数形结合、化归与转化思想,是中档题.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源: 题型:选择题
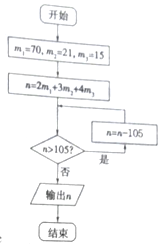 明朝数学家程大位将“孙子定理”(也称“中国剩余定理”)编成易于上口的《孙子歌诀》:三人同行七十稀,五树梅花廿一支,七子团圆正半月,除百零五便得知.已知正整数n被3除余2,被5除余3,被7除余4,求n的最小值.按此歌诀得算法如图,则输出n的结果为( )
明朝数学家程大位将“孙子定理”(也称“中国剩余定理”)编成易于上口的《孙子歌诀》:三人同行七十稀,五树梅花廿一支,七子团圆正半月,除百零五便得知.已知正整数n被3除余2,被5除余3,被7除余4,求n的最小值.按此歌诀得算法如图,则输出n的结果为( )| A. | 53 | B. | 54 | C. | 158 | D. | 263 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在平面直角坐标系xOy中,以x轴正半轴为始边的锐角α与钝角β的终边与单位圆分别交于点A,B两点,x轴正半轴与单位圆交于点M,已知${S_{△OAM}}=\frac{{\sqrt{5}}}{5}$,点B的纵坐标是$\frac{{\sqrt{2}}}{10}$,
如图,在平面直角坐标系xOy中,以x轴正半轴为始边的锐角α与钝角β的终边与单位圆分别交于点A,B两点,x轴正半轴与单位圆交于点M,已知${S_{△OAM}}=\frac{{\sqrt{5}}}{5}$,点B的纵坐标是$\frac{{\sqrt{2}}}{10}$,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
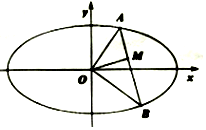 如图,在椭圆$C:\frac{x^2}{4}+{y^2}=1$中,过坐标原点O作两条互相垂直的射线OA,OB与C分别交于A,B两点.
如图,在椭圆$C:\frac{x^2}{4}+{y^2}=1$中,过坐标原点O作两条互相垂直的射线OA,OB与C分别交于A,B两点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{7}}{4}$ | B. | $\frac{\sqrt{7}}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com