
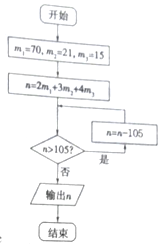
 明朝数学家程大位将“孙子定理”(也称“中国剩余定理”)编成易于上口的《孙子歌诀》:三人同行七十稀,五树梅花廿一支,七子团圆正半月,除百零五便得知.已知正整数n被3除余2,被5除余3,被7除余4,求n的最小值.按此歌诀得算法如图,则输出n的结果为( )
明朝数学家程大位将“孙子定理”(也称“中国剩余定理”)编成易于上口的《孙子歌诀》:三人同行七十稀,五树梅花廿一支,七子团圆正半月,除百零五便得知.已知正整数n被3除余2,被5除余3,被7除余4,求n的最小值.按此歌诀得算法如图,则输出n的结果为( )| A. | 53 | B. | 54 | C. | 158 | D. | 263 |
科目:高中数学 来源: 题型:选择题
| A. | -2016 | B. | -2017 | C. | 2017 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
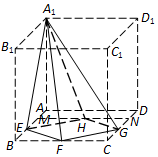 如图,在正方体ABCD-A1B1C1D1中,M、E是AB的三等分点,G、N是CD的三等分点,F、H分别是BC、MN的中点,则四棱锥A1-EFGH的左视图是( )
如图,在正方体ABCD-A1B1C1D1中,M、E是AB的三等分点,G、N是CD的三等分点,F、H分别是BC、MN的中点,则四棱锥A1-EFGH的左视图是( )| A. | 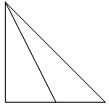 | B. | 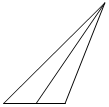 | C. | 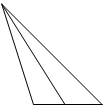 | D. | 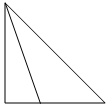 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
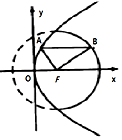 如图所示点F是抛物线y2=8x的焦点,点A、B分别在抛物线y2=8x及圆x2+y2-4x-12=0的实线部分上运动,且AB总是平行于x轴,则△FAB的周长的取值范围是( )
如图所示点F是抛物线y2=8x的焦点,点A、B分别在抛物线y2=8x及圆x2+y2-4x-12=0的实线部分上运动,且AB总是平行于x轴,则△FAB的周长的取值范围是( )| A. | (6,10) | B. | (8,12) | C. | [6,8] | D. | [8,12] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{3}+1$ | D. | $2\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,1) | B. | (-∞,1) | C. | (0,1) | D. | (-2,0] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
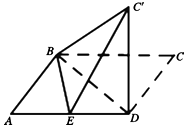 已知平行四边形ABCD中,AB=6,AD=10,BD=8,E是线段AD的中点.沿BD将△BCD翻折到△BC'D,使得平面BC'D⊥平面ABD.
已知平行四边形ABCD中,AB=6,AD=10,BD=8,E是线段AD的中点.沿BD将△BCD翻折到△BC'D,使得平面BC'D⊥平面ABD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com