
| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{3}+1$ | D. | $2\sqrt{3}$ |
分析 由题意可得A在双曲线的右支上,由双曲线的定义可得|AF1|-|AF2|=2a,设Rt△AF1F2内切圆半径为r,运用等积法和勾股定理,可得r=c-a,结合条件和离心率公式,计算即可得到所求值.
解答 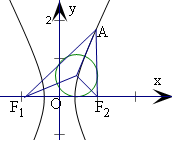 解:由点A在双曲线上,且AF2⊥x轴,
解:由点A在双曲线上,且AF2⊥x轴,
可得A在双曲线的右支上,
由双曲线的定义可得|AF1|-|AF2|=2a,
设Rt△AF1F2内切圆半径为r,
运用面积相等可得S${\;}_{△A{F}_{1}{F}_{2}}$=$\frac{1}{2}$|AF2|•|F1F2|
=$\frac{1}{2}$r(|AF1|+|AF2|+|F1F2|),
由勾股定理可得|AF2|2+|F1F2|2=|AF1|2,
解得r=$\frac{{|{A{F_2}}|+|{{F_1}{F_2}}|-|{A{F_1}}|}}{2}=\frac{2c-2a}{2}=c-a=({\sqrt{3}-1})a$,
$⇒c=\sqrt{3}a$,
则离心率e=$\frac{c}{a}$=$\sqrt{3}$,
故选A.
点评 本题考查双曲线的离心率的求法,注意运用双曲线的定义和三角形的等积法,考查化简整理的运算能力,属于中档题.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案科目:高中数学 来源: 题型:选择题
| A. | {0} | B. | {1,2,3} | C. | {0,4} | D. | {4} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
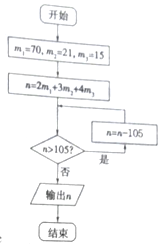 明朝数学家程大位将“孙子定理”(也称“中国剩余定理”)编成易于上口的《孙子歌诀》:三人同行七十稀,五树梅花廿一支,七子团圆正半月,除百零五便得知.已知正整数n被3除余2,被5除余3,被7除余4,求n的最小值.按此歌诀得算法如图,则输出n的结果为( )
明朝数学家程大位将“孙子定理”(也称“中国剩余定理”)编成易于上口的《孙子歌诀》:三人同行七十稀,五树梅花廿一支,七子团圆正半月,除百零五便得知.已知正整数n被3除余2,被5除余3,被7除余4,求n的最小值.按此歌诀得算法如图,则输出n的结果为( )| A. | 53 | B. | 54 | C. | 158 | D. | 263 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=±x | B. | $y=±\frac{2}{3}x$ | C. | $y=±\frac{1}{3}x$ | D. | $y=±\frac{1}{2}x$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,2) | B. | (-2,2) | C. | (-2,3] | D. | [-1,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 数列{xi}可能是等比数列 | B. | 数列{yi}是常数列 | ||
| C. | 数列{xi}可能是等差数列 | D. | 数列{xi+yi }可能是等比数列 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com