
| A. | 数列{xi}可能是等比数列 | B. | 数列{yi}是常数列 | ||
| C. | 数列{xi}可能是等差数列 | D. | 数列{xi+yi }可能是等比数列 |
分析 由直线ax+by+ci=0,对系数a,b分类讨论,利用中点坐标公式可得M坐标,再利用等差数列与等比数列的定义通项公式即可判断出结论.
解答 解:由直线ax+by+ci=0,当a=0,b≠0时,直线by+ci=0与抛物线y2=2px(p>0)仅有一个交点,不合题意.
当a≠0,b=0时,直线ax+ci=0,化为:x=-$\frac{{c}_{i}}{a}$,则xi=-$\frac{{c}_{i}}{a}$,yi=0,xi+yi=-$\frac{{c}_{i}}{a}$,
由{ci}(i∈N*)是公比不为1的等比数列,可得{xi }是等比数列,{xi+yi }是等比数列,不是等差数列.
当a≠0,b≠0时,直线ax+by+ci=0化为:x=-$\frac{b}{a}$y-$\frac{{c}_{i}}{a}$,代入抛物线y2=2px(p>0),∴y2+$\frac{2pb}{a}$y+$\frac{2p{c}_{i}}{a}$=0.
根据根与系数的关系可得:$(\frac{p{b}^{2}}{{a}^{2}}-\frac{{c}_{i}}{a},-\frac{pb}{a})$.{yi }是常数列,是等比数列,是等差数列.
综上可得:A,B,D都有可能,只有C不可能.
故选:C.
点评 本题考查了直线方程、直线与抛物线相交问题、中点坐标公式、一元二次方程的根与系数的关系、等差数列与等比数列的定义通项公式,考查了推理能力与计算能力,属于难题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{3}+1$ | D. | $2\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | α<θ<β | B. | β<θ<α | C. | β<α<θ | D. | α<β<θ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,1) | B. | (-∞,1) | C. | (0,1) | D. | (-2,0] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,1) | B. | (-1,+∞) | C. | (-1,1)∪[2,+∞) | D. | ∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
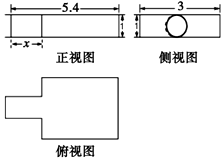 我国古代数学名著《九章算术》中记载了公元前344年商鞅督造一种标准量器商鞅铜方升,其三视图如图所示(单位:寸),若π取3,且图中的x为1.6(寸).则其体积为( )
我国古代数学名著《九章算术》中记载了公元前344年商鞅督造一种标准量器商鞅铜方升,其三视图如图所示(单位:寸),若π取3,且图中的x为1.6(寸).则其体积为( )| A. | 0.4π+11.4立方寸 | B. | 13.8立方寸 | C. | 12.6立方寸 | D. | 16.2立方寸 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com