
分析 由约束条件作出可行域,对a分类可得a>0,然后求出三角形的顶点坐标,由边长相等列式求得a值.
解答 解:由约束条件$\left\{\begin{array}{l}x+2y-4≤0\\ ax+3y-4≥0\\ y≥0\end{array}\right.$作出可行域如图,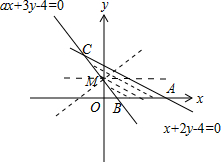
若a≤0,则约束条件表示的平面区域不是三角形,不合题意;
若a>0,联立$\left\{\begin{array}{l}{ax+3y-4=0}\\{x+2y-4=0}\end{array}\right.$,解得C($\frac{4}{3-2a}$,$\frac{4-4a}{3-2a}$),
又B($\frac{4}{a},0$),
由题意可得:$\sqrt{(\frac{4}{3-2a}-\frac{4}{a})^{2}+(\frac{4-4a}{3-2a})^{2}}=4-\frac{4}{a}$,解得a=4.
故答案为:4.
点评 本题考查简单的线性规划,考查数形结合的解题思想方法,是中档题.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 36种 | B. | 30种 | C. | 24种 | D. | 12种 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=±x | B. | $y=±\frac{2}{3}x$ | C. | $y=±\frac{1}{3}x$ | D. | $y=±\frac{1}{2}x$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 数列{xi}可能是等比数列 | B. | 数列{yi}是常数列 | ||
| C. | 数列{xi}可能是等差数列 | D. | 数列{xi+yi }可能是等比数列 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
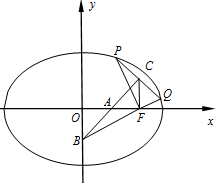 已知椭圆M:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的右焦点F的坐标为(1,0),P,Q为椭圆上位于y轴右侧的两个动点,使PF⊥QF,C为PQ中点,线段PQ的垂直平分线交x轴,y轴于点A,B(线段PQ不垂直x轴),当Q运动到椭圆的右顶点时,$|PF|=\frac{{\sqrt{2}}}{2}$.
已知椭圆M:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的右焦点F的坐标为(1,0),P,Q为椭圆上位于y轴右侧的两个动点,使PF⊥QF,C为PQ中点,线段PQ的垂直平分线交x轴,y轴于点A,B(线段PQ不垂直x轴),当Q运动到椭圆的右顶点时,$|PF|=\frac{{\sqrt{2}}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({-e,-\sqrt{e}})$ | B. | $({-2\sqrt{e},-e})$ | C. | $({-\sqrt{e},0})$ | D. | $[-e,-\frac{e}{2})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com