
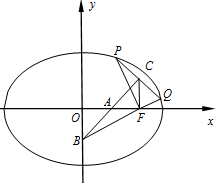
 已知椭圆M:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的右焦点F的坐标为(1,0),P,Q为椭圆上位于y轴右侧的两个动点,使PF⊥QF,C为PQ中点,线段PQ的垂直平分线交x轴,y轴于点A,B(线段PQ不垂直x轴),当Q运动到椭圆的右顶点时,$|PF|=\frac{{\sqrt{2}}}{2}$.
已知椭圆M:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的右焦点F的坐标为(1,0),P,Q为椭圆上位于y轴右侧的两个动点,使PF⊥QF,C为PQ中点,线段PQ的垂直平分线交x轴,y轴于点A,B(线段PQ不垂直x轴),当Q运动到椭圆的右顶点时,$|PF|=\frac{{\sqrt{2}}}{2}$.分析 (Ⅰ) 当Q运动到椭圆的右顶点时,PF⊥x轴,$|PF|=\frac{b^2}{a}=\frac{{\sqrt{2}}}{2}$,又c=1,a2=b2+c2,解出即可得出.
(Ⅱ)设直线PQ的方程为y=kx+b,显然k≠0,联立椭圆方程得:(2k2+1)x2+4kbx+2(b2-1)=0,设点P(x1,y1),Q(x1,y1),根据根与系数的关系$\overrightarrow{PF}•\overrightarrow{QF}=0⇒({x_1}-1)({x_2}-1)+{y_1}{y_2}=0$得:3b2-1+4kb=0,点$C({\frac{-2kb}{{2{k^2}+1}},\frac{b}{{2{k^2}+1}}})$,线段PQ的中垂线AB方程:$y-\frac{-kb}{{2{k^2}+1}}=-\frac{1}{k}({x+\frac{b}{{2{k^2}+1}}})$.可得A,B的坐标.$\frac{{{S_{△BCF}}}}{{{S_{△ABO}}}}=\frac{{2{S_{△ABF}}}}{{{S_{△ABO}}}}=2\frac{|AF|}{|AO|}=\frac{{2(1-{x_A})}}{x_A}=2({\frac{1}{x_A}-1})$,进而得出.
解答 解:(Ⅰ) 当Q运动到椭圆的右顶点时,PF⊥x轴,∴$|PF|=\frac{b^2}{a}=\frac{{\sqrt{2}}}{2}$,
又c=1,a2=b2+c2,∴$a=\sqrt{2},b=1$.
椭圆M的标准方程为:$\frac{x^2}{2}+{y^2}=1$
(Ⅱ)设直线PQ的方程为y=kx+b,显然k≠0,
联立椭圆方程得:(2k2+1)x2+4kbx+2(b2-1)=0,
设点P(x1,y1),Q(x1,y1),
由韦达定理:$\left\{\begin{array}{l}{x_1}{x_2}=\frac{{2({b^2}-1)}}{{2{k^2}+1}}>0,(1)\\{x_1}+{x_2}=\frac{-4kb}{{2{k^2}+1}}>0,(2)\\△=8(2{k^2}-{b^2}+1)>0,(3)\end{array}\right.$
由$\overrightarrow{PF}•\overrightarrow{QF}=0⇒({x_1}-1)({x_2}-1)+{y_1}{y_2}=0$得:3b2-1+4kb=0 (4)
点$C({\frac{-2kb}{{2{k^2}+1}},\frac{b}{{2{k^2}+1}}})$,
∴线段PQ的中垂线AB方程:$y-\frac{-kb}{{2{k^2}+1}}=-\frac{1}{k}({x+\frac{b}{{2{k^2}+1}}})$,
令x=0,y=0可得:$A({\frac{-kb}{{2{k^2}+1}},0}),B({0,\frac{-b}{{2{k^2}+1}}})$,则A为BC中点,
故$\frac{{{S_{△BCF}}}}{{{S_{△ABO}}}}=\frac{{2{S_{△ABF}}}}{{{S_{△ABO}}}}=2\frac{|AF|}{|AO|}=\frac{{2(1-{x_A})}}{x_A}=2({\frac{1}{x_A}-1})$,
由(4)式得:$k=\frac{{1-3{b^2}}}{4b}$,则${x_A}=\frac{-kb}{{2{k^2}+1}}=\frac{{6{b^4}-2{b^2}}}{{9{b^4}+2{b^2}+1}}$$\frac{{{S_{△BCF}}}}{{{S_{△ABO}}}}=2({\frac{1}{x_A}-1})=\frac{{6{b^4}+8{b^2}+2}}{{6{b^4}-2{b^2}}}=\frac{5}{3}$,得:b2=3.
∴b=$\sqrt{3}$,k=-$\frac{2\sqrt{3}}{3}$或b=-$\sqrt{3}$,k=$\frac{2\sqrt{3}}{3}$.
经检验,满足条件(1)(2)(3),
故直线PQ的方程为:y=$\frac{2\sqrt{3}}{3}$x-$\sqrt{3}$,y=-$\frac{2\sqrt{3}}{3}$x+$\sqrt{3}$.
点评 本题考查了椭圆的标准方程及其性质、一元二次方程的根与系数的关系、垂直平分线的性质、中点坐标公式,考查了推理能力与计算能力,属于难题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{4}{5}$ | C. | $\frac{8}{9}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | $\frac{{\sqrt{5}}}{2}$ | C. | $\sqrt{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
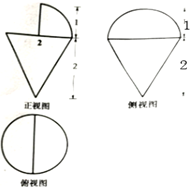
| A. | π | B. | $\frac{4π}{3}$ | C. | $\frac{7π}{3}$ | D. | $\frac{8π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
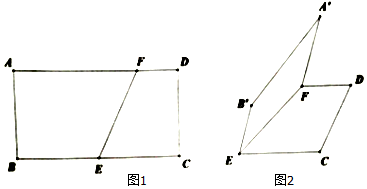
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com