
分析 (1)当a=1,c=2,b=3时,f(x)=|2x+1|+|2x-3|,分类讨论,即可解方程f(x)-4=0;
(2)当c=1,b=1时,f(x)=|x-1|+|x+a|,g(x)=|x-2|+1,对任意x1∈R,都存在x2∈R,使得g(x2)=f(x1)成立,{y|y=f(x)}⊆{y|y=g(x)}.
解答 解:(1)当a=1,c=2,b=3时,f(x)=|2x+1|+|2x-3|,…(2分)
∴原方程等价于$\left\{\begin{array}{l}x<-\frac{1}{2}\\-4x+2-4=0\end{array}\right.$或$\left\{\begin{array}{l}-\frac{1}{2}≤x≤\frac{3}{2}\\ 4-4=0\end{array}\right.$或$\left\{\begin{array}{l}x>\frac{3}{2}\\ 4x-2-4=0\end{array}\right.$
解得:∅或$-\frac{1}{2}≤x≤\frac{3}{2}$或∅.
即方程f(x)-4=0的解为$\left\{{\left.x\right|-\frac{1}{2}≤x≤\frac{3}{2}}\right\}$…(5分)
(2)当c=1,b=1时,f(x)=|x-1|+|x+a|,g(x)=|x-2|+1,
∵对任意x1∈R,都存在x2∈R,使得g(x2)=f(x1)成立,
∴{y|y=f(x)}⊆{y|y=g(x)},…(6分)
f(x)=|x-1|+|x+a|≥|(x-1)-(x+a)|=|a+1|,
(当且仅当(x-1)(x+1)≤0时等号成立),g(x)=|x-2|+1≥1,所以|a+1|≥1,…(8分)
∴a+1≥1或a+1≤-1,
∴a≥0或a≤-2,∴实数a的取值范围为(-∞,-2]∪[0,+∞). …(10分)
点评 本题考查了解绝对值不等式问题,考查集合的包含关系,是一道中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
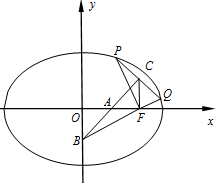 已知椭圆M:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的右焦点F的坐标为(1,0),P,Q为椭圆上位于y轴右侧的两个动点,使PF⊥QF,C为PQ中点,线段PQ的垂直平分线交x轴,y轴于点A,B(线段PQ不垂直x轴),当Q运动到椭圆的右顶点时,$|PF|=\frac{{\sqrt{2}}}{2}$.
已知椭圆M:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的右焦点F的坐标为(1,0),P,Q为椭圆上位于y轴右侧的两个动点,使PF⊥QF,C为PQ中点,线段PQ的垂直平分线交x轴,y轴于点A,B(线段PQ不垂直x轴),当Q运动到椭圆的右顶点时,$|PF|=\frac{{\sqrt{2}}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({-e,-\sqrt{e}})$ | B. | $({-2\sqrt{e},-e})$ | C. | $({-\sqrt{e},0})$ | D. | $[-e,-\frac{e}{2})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,x2-1≤0 | B. | ?x∈R,x2-1>0 | C. | ?x0∈R,x02-1>0 | D. | ?x0∈R,x02-1<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
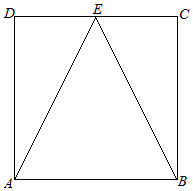 如图,点E是边长为2的正方形ABCD的CD边中点,若向正方形ABCD内随机投掷一点,则所投点落在△ABE内的概率为( )
如图,点E是边长为2的正方形ABCD的CD边中点,若向正方形ABCD内随机投掷一点,则所投点落在△ABE内的概率为( )| A. | $\frac{\sqrt{3}}{4}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 10 | 15 | 17 | 20 | 25 | 28 | 32 |
| y | 1 | 1.3 | 1.8 | 2 | 2.6 | 2.7 | 3.3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com