练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    2．已知集合A={x|2x2-7x＜0}，B={0，1，2，3，4}，则（∁RA）∩B=（　　）
    A．{0}B．{1，2，3}C．{0，4}D．{4}

    分析 解不等式得集合A，根据补集与交集的定义写出（∁RA）∩B即可．

    解答 解：集合A={x|2x2-7x＜0}={x|0＜x＜$\frac{7}{2}$}，
    ∴∁RA={x|x≤0或x≥$\frac{7}{2}$}，
    又B={0，1，2，3，4}，
    ∴（∁RA）∩B={0，4}．
    故选：C．

    点评 本题考查了解不等式与集合的运算问题，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    12．下列说法正确的是（　　）
    A．存在x0∈R，使得$1-{cos^3}{x_0}={log_2}\frac{1}{10}$
    B．函数y=sin2xcos2x的最小正周期为π
    C．函数$y=cos2（{x+\frac{π}{3}}）$的一个对称中心为$（{-\frac{π}{3}，0}）$
    D．角α的终边经过点（cos（-3），sin（-3）），则角α是第三象限角

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．设函数$f（x）=2alnx+\frac{lnx}{x}$．
    （Ⅰ）若$a=-\frac{1}{2}$，求f（x）的极值；
    （Ⅱ）若f（x）在定义域上单调递增，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．已知点P为函数f（x）=ex的图象上任意一点，点Q为圆（x-e2-1）2+y2=1上任意一点（e为自然对数的底），则线段PQ的长度的最小值为$e\sqrt{{e^2}+1}-1$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．已知等差数列{an}的前n项和为Sn，设A（a1009，1），B（2，-1），C（2，2）为坐标平面上三点，O为坐标原点，若向量$\overrightarrow{OA}$与$\overrightarrow{OB}$在向量$\overrightarrow{OC}$方向上的投影相同，则S2017为（　　）
    A．-2016B．-2017C．2017D．0

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．将函数f（x）=sinπx的图象向左平移$\frac{1}{2}$个单位后得到函数g（x）的图象，若f（x）和g（x）在区间[-1，2]上的图象交于A，B，C三点，则△ABC的面积是（　　）
    A．$\frac{\sqrt{2}}{2}$B．$\frac{3\sqrt{2}}{4}$C．$\sqrt{2}$D．$\frac{5\sqrt{2}}{4}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

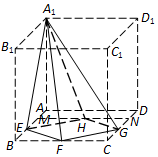    14．如图，在正方体ABCD-A1B1C1D1中，M、E是AB的三等分点，G、N是CD的三等分点，F、H分别是BC、MN的中点，则四棱锥A1-EFGH的左视图是（　　）
    A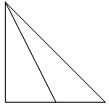．B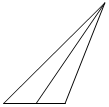．C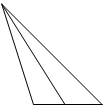．D．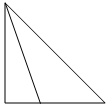

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（{a＞0，b＞0}）$的左，右焦点分别为F1，F2，点A在双曲线上，且AF2⊥x轴，若△AF1F2的内切圆半价为$（{\sqrt{3}-1}）a$，则其离心率为（　　）
    A．$\sqrt{3}$B．2C．$\sqrt{3}+1$D．$2\sqrt{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．若集合A=$\left\{{x|-1＜x＜1，x∈R}\right\}，B=\left\{{x|y=\sqrt{x-2}，x∈R}\right\}$，则A∪B=（　　）
    A．[0，1）B．（-1，+∞）C．（-1，1）∪[2，+∞）D．∅

    查看答案和解析>>

    同步练习册答案