
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 先根据折线距离的定义分别表示出所求的集合,然后根据集合中绝对值的性质进行判定即可.
解答 解:若点C在线段AB上,设C点坐标为(x0,y0),x0在x1、x2之间,y0在y1、y2之间,
则d(A,C)+d(C,B)=|x0-x1|+|y0-y1|+|x2-x0|+|y2-y0|=|x2-x1|+|y2-y1|=d(A,B)成立,故①正确;
在△ABC中,d(A,C)+d(C,B)=|x0-x1|+|y0-y1|+|x2-x0|+|y2-y0|≥|(x0-x1)+(x2-x0)|+|(y0-y1)+(y2-y0)|=|x2-x1|+|y2-y1|=d(A,B)③,故②错误;
到M(-1,0),N(1,0)两点的“折线距离”相等点的集合是{(x,y)||x+1|+|y|=|x-1|+|y|},
由|x+1|=|x-1|,解得x=0,
∴到M(-1,0),N(1,0)两点的“折线距离”相等的点的轨迹方程是x=0,即③成立;
设B(x,y),则d(A,B)=|x1-x2|+|y1-y2|=|x|+|2$\sqrt{5}$-x|≥2$\sqrt{5}$,即d(A,B)的最小值为2$\sqrt{5}$,故④正确;
综上知,正确的命题为①③④,共3个.
故选:C.
点评 本题主要考查了“折线距离”的定义,考查分析问题、解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | -$\frac{5}{2}$i | B. | -$\frac{5}{2}$ | C. | $\frac{5}{2}$i | D. | $\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{5}$ | C. | $\sqrt{10}$ | D. | 2$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
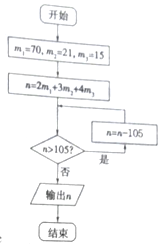 明朝数学家程大位将“孙子定理”(也称“中国剩余定理”)编成易于上口的《孙子歌诀》:三人同行七十稀,五树梅花廿一支,七子团圆正半月,除百零五便得知.已知正整数n被3除余2,被5除余3,被7除余4,求n的最小值.按此歌诀得算法如图,则输出n的结果为( )
明朝数学家程大位将“孙子定理”(也称“中国剩余定理”)编成易于上口的《孙子歌诀》:三人同行七十稀,五树梅花廿一支,七子团圆正半月,除百零五便得知.已知正整数n被3除余2,被5除余3,被7除余4,求n的最小值.按此歌诀得算法如图,则输出n的结果为( )| A. | 53 | B. | 54 | C. | 158 | D. | 263 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -4 | C. | $-\frac{3}{4}$ | D. | $-\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,2) | B. | (-2,2) | C. | (-2,3] | D. | [-1,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在平面直角坐标系xOy中,以x轴正半轴为始边的锐角α与钝角β的终边与单位圆分别交于点A,B两点,x轴正半轴与单位圆交于点M,已知${S_{△OAM}}=\frac{{\sqrt{5}}}{5}$,点B的纵坐标是$\frac{{\sqrt{2}}}{10}$,
如图,在平面直角坐标系xOy中,以x轴正半轴为始边的锐角α与钝角β的终边与单位圆分别交于点A,B两点,x轴正半轴与单位圆交于点M,已知${S_{△OAM}}=\frac{{\sqrt{5}}}{5}$,点B的纵坐标是$\frac{{\sqrt{2}}}{10}$,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{7}}{4}$ | B. | $\frac{\sqrt{7}}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com