
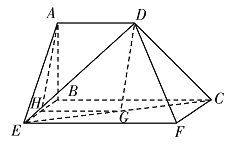
【题目】下面是几何体![]() 的三视图及直观图.
的三视图及直观图.

(1)试判断线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ,请说明理由;
,请说明理由;
(2)证明:![]() .
.
【答案】(1)见解析;(2)见解析
【解析】分析:(1)取BC与EC的中点H,G,可证HG与AD平行且相等,从而得ADGH是平行四边形,因此有AH//DG,从而得线面平行;
(2)由题中条件证明垂直后计算出![]() 的长度,再用勾股定理逆定理证得
的长度,再用勾股定理逆定理证得![]() .
.
详解: (1)存在线段![]() 的中点
的中点![]() ,使得
,使得![]() 平面
平面![]() ,理由如下:
,理由如下:
由三视图可知,![]() ,且
,且![]() 平面
平面![]() ,
,![]() 平面
平面![]()
取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,
因为![]() 为
为![]() 中点,所以
中点,所以![]()
![]() ,且
,且![]()
因为四边形![]() 是直角梯形,
是直角梯形,![]() ,且
,且![]() ,
,
所以![]() ,所以四边形
,所以四边形![]() 为平行四边形,所以
为平行四边形,所以![]()
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)因为![]() 平面
平面![]() ,所以
,所以![]() ,
,
所以![]() ,因为四边形
,因为四边形![]() 为矩形,
为矩形,
所以![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() ,
,
又![]() ,故
,故![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() ,故
,故![]() ,
,
因为四边形![]() 为直角梯形,
为直角梯形,![]() ,且
,且![]() ,
,
所以![]() ,∴
,∴![]() .
.
又![]() ,即
,即![]() ,故
,故![]() .
.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源: 题型:
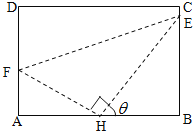
【题目】如图,某污水处理厂要在一个矩形污水处理池![]() 的池底水平铺设污水净化管道(
的池底水平铺设污水净化管道(![]() ,
,![]() 是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口
是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口![]() 是
是![]() 的中点,
的中点,![]() 分别落在线段
分别落在线段![]() 上.已知
上.已知![]() 米,
米,![]() 米,记
米,记![]() .
.
(1)试将污水净化管道的长度![]() 表示为
表示为![]() 的函数,并写出定义域;
的函数,并写出定义域;
(2)若![]() ,求此时管道的长度
,求此时管道的长度![]() ;
;
(3)当![]() 取何值时,污水净化效果最好?并求出此时管道的长度.
取何值时,污水净化效果最好?并求出此时管道的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】复利是一种计算利息的方法.即把前一期的利息和本金加在一起算作本金,再计算下一期的利息.某同学有压岁钱1000元,存入银行,年利率为2.25%;若放入微信零钱通或
者支付宝的余额宝,年利率可达4.01%.如果将这1000元选择合适方式存满5年,可以多获利息( )元.(参考数据:![]() )
)
A. 176 B. 100 C. 77 D. 88
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为调查高三年学生的身高情况,按随机抽样的方法抽取80名学生,得到男生身高情况的频率分布直方图(图(1))和女生身高情况的频率分布直方图(图(2)).已知图(1)中身高在170~175cm的男生人数有16人.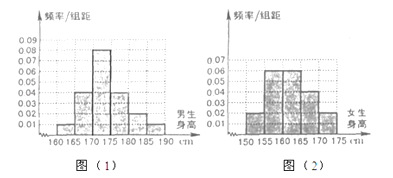
(Ⅰ)试问在抽取的学生中,男、女生各有多少人?
(Ⅱ)根据频率分布直方图,完成下列的2×2列联表,并判断能有多大(百分几)的把握认为“身高与性别有关”?
≥170cm | <170cm | 总计 | |
男生身高 | |||
女生身高 | |||
总计 |
(Ⅲ)在上述80名学生中,从身高在170~175cm之间的学生中按男、女性别分层抽样的方法,抽出5人,从这5人中选派3人当旗手,求3人中恰好有一名女生的概率.
参考公式:K2=![]()
参考数据:
P(K2≥k0) | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设样本数据x1 , x2 , …,x10的均值和方差分别为1和4,若yi=xi+a(a为非零常数,i=1,2,…,10),则y1 , y2 , …,y10的均值和方差分别为( )
A.1+a,4
B.1+a,4+a
C.1,4
D.1,4+a
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).在以原点
为参数).在以原点![]() 为极点,
为极点,![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域为
的定义域为![]() ,部分对应值如下表,
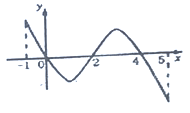
,部分对应值如下表,![]() 的导函数
的导函数![]() 的图象如图所示,给出关于
的图象如图所示,给出关于![]() 的下列命题:
的下列命题:
①函数![]() 在
在![]() 处取得极小值;
处取得极小值;
②函数![]() 在
在![]() 是减函数,在
是减函数,在![]() 是增函数;
是增函数;
③当![]() 时,函数
时,函数![]() 有4个零点;
有4个零点;
④如果当![]() 时,
时,![]() 的最大值是2,那么
的最大值是2,那么![]() 的最小值为0.
的最小值为0.
其中所有的正确命题是__________(写出正确命题的序号).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com