
����Ŀ����������ҵ�IJ��Ϸ�չ���г�����Խ��Խ���ң��˿Ͷ����з���������Ҫ��Խ��Խ�ߣ�����Ϊ����߹�Ա��Ա���ķ�����ʶ����ǿ���۹������������ù˿ͶԷ����������ۣ����۷�Ϊ���⡢�������⡢���������֣�ij����Ϊ�˱ȽϹ˿Ͷ���Ů��ԱԱ����������۵IJ��죬���������ĸ�������������40�ˣ���Ů���룩���з����Ƚ϶�40��һ���еĹ˿����������������Ĵ���������ͳ�ƣ����С�Ů��Ϊ���飬�ٽ�ÿ���ԱԱ����������������������Ϊ5�飺[0��5����[5��10����[10��15����[15��20����[20��25]���õ�����Ƶ���ֲ�����
���� | [0��5�� | [5��10�� | [10��15�� | [15��20�� | [20��25] |
Ů��Ա | 2 | 3 | 8 | 5 | 2 |
�й�Ա | 1 | 3 | 9 | 4 | 3 |
��1���ڴ������������ϵ�зֱ��С�Ů��ԱԱ����Ƶ�ʷֲ�ֱ��ͼ��������С�Ů��Ա����ƽ�����������������Ĺ���ֵ���Ը��ݹ���ֵ�Ƚ��С�Ů��Ա�������˭�ߣ�
��2���ڳ�ȡ��40����ԱԱ���У�����������������������20�Ĺ�ԱԱ���������ȡ3�ˣ����ȡ��3���У��й�Ա������Ů��Ա�ĸ��ʣ�
���𰸡���1����������13��13.75��Ů��ԱԱ���������Ҫ�ߣ���2��![]() ��
��
��������
��1���ֱ��г�Ů��Ա���й�Ա��Ƶ�ʷֲ������ٻ���Ů��Ա���й�Ա��Ƶ�ʷֲ�ֱ��ͼ������Ů��Ա���й�ԱԱ������ƽ���������⡱�������Ƚϼ��ɵó����ۣ���2���������⡱����������20�Ĺ�ԱԱ������5�ˣ�����ŮԱ��2�ˣ���Ա��3�ˣ��ӡ������⡱����������20�Ĺ�ԱԱ���������ȡ3�ˣ������¼�����![]() ����ȡ��3���У��й�Ա������Ů��Ա�����Ļ����¼�����
����ȡ��3���У��й�Ա������Ů��Ա�����Ļ����¼�����![]() ���ɴ��������ȡ��3���У��й�Ա������Ů��Ա�ĸ��ʣ�
���ɴ��������ȡ��3���У��й�Ա������Ů��Ա�ĸ��ʣ�
��1������Ů��Ա�г�Ƶ�ʷֲ������£�
���� | [0��5�� | [5��10�� | [10��15�� | [15��20�� | [20��25] |
Ů��Ա | 2 | 3 | 8 | 5 | 2 |
Ƶ�� | 0.1 | 0.15 | 0.4 | 0.25 | .0.1 |
�����й�Ա�г�Ƶ�ʷֲ������£�
���� | [0��5�� | [5��10�� | [10��15�� | [15��20�� | [20��25] |
�й�Ա | 1 | 3 | 9 | 4 | 3 |
�й�Ա | 0.05 | 0.15 | 0.45 | 0.2 | 0.15 |
�ֱ�Ů��Ա���й�Ա��Ƶ�ʷֲ�ֱ��ͼ����ͼ��ʾ��
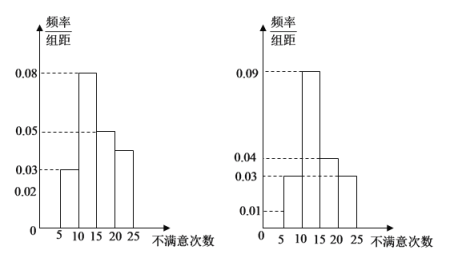
��Ů��Ա���й�ԱԱ������ƽ�����������������ֱ�Ϊ![]() ��
��![]() ��
��
��![]() ��2��2.5+3��7.5+8��12.5+5��17.5+2��22.5��
��2��2.5+3��7.5+8��12.5+5��17.5+2��22.5��![]() 260��13��
260��13��
![]() ��1��2.5+3��7.5+9��12.5+4��17.5+3��22.5��
��1��2.5+3��7.5+9��12.5+4��17.5+3��22.5��![]() 275��13.75��
275��13.75��
��![]() ����Ů��ԱԱ���������Ҫ�ߣ�
����Ů��ԱԱ���������Ҫ�ߣ�
��2���ڳ�ȡ��40����ԱԱ���У�
��������������������20�Ĺ�ԱԱ������5�ˣ�����ŮԱ��2�ˣ���Ա��3�ˣ�
����������������������20�Ĺ�ԱԱ���������ȡ3�ˣ�
�����¼�����![]() ��
��
��ȡ��3���У��й�Ա������Ů��Ա�����Ļ����¼�������
m![]() 7��
7��
���ȡ��3���У��й�Ա������Ů��Ա�ĸ���p![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧΪ�������ѧ��Ӣ������ˮƽ������������ȡ�˸����꼶��80��ѧ�����в��ԣ����ݲ��Խ��������Ӣ�������ɼ�������Ϊ30�֣���Ƶ�ʷֲ�ֱ��ͼ�����ɼ�������27�ֵĶ�Ϊ����
��1��������֪������������![]() �����������ݴ������ж��Ƿ���90%�İ�����ΪӢ�������ɼ��Ƿ��������Ա��йأ�
�����������ݴ������ж��Ƿ���90%�İ�����ΪӢ�������ɼ��Ƿ��������Ա��йأ�
Ӣ���������� | ��Ӣ���������� | �ϼ� | |
��ͬѧ | 10 | ||
Ůͬѧ | 36 | ||
�ϼ� |
��2���������������õ���Ƶ����Ϊ���ʣ����ڴӸ�У����ѧ���У���ȡ�����������ÿ�γ�ȡ1��ѧ��������ȡ3�Σ��DZ���ȡ��3��ѧ������Ӣ������������������ΪX����ÿ�γ�ȡ�Ľ����������ģ���X�ķֲ��к���ѧ����E��X��
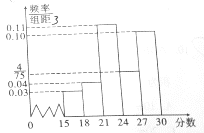
�ο���ʽ��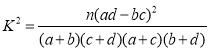 ������
������![]()
�ο��ٽ�ֵ��
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ���������ֲһ�����ÿ����ֲ�ɱ�Ϊ1000Ԫ����������г��۸�������ϵIJ�������������ԣ��һ���Ӱ�죬�����������±���
��������� | 400 | 500 |
���� |
|
|
�����г��۸�Ԫ/ | 5 | 6 |
���� |
|
|
��1����![]() ��ʾ����������ֲ1���������������
��ʾ����������ֲ1���������������![]() �ķֲ��У�����
�ķֲ��У�����![]() ����
����![]() �г��۸�
�г��۸�![]() �ɱ�����
�ɱ�����
��2����������������3����ֲ���������3���е�����������![]() �ĸ���.
�ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x����ex![]() ��
��
��1����f��x����ͼ����x��a�����ߵ�б��Ϊe��1��������a��ֵ��
��2���������a��0��f��x����2lnx![]() k�������������k�����ֵ��
k�������������k�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ĸ↑�����������ǵ�֧����ʽ�����˾�ת�䣮���������ƶ�֧���ѳ�Ϊ��Ҫ֧����ʽ֮һ��Ϊ�˽�ijУѧ���ϸ���A��B�����ƶ�֧����ʽ��ʹ���������ȫУѧ���������ȡ��100�ˣ�����������A��B����֧����ʽ����ʹ�õ���5�ˣ������н�ʹ��A�ͽ�ʹ��B��ѧ����֧�����ֲ�������£�
֧����ʽ | ��0,1000] | ��1000,2000] | ����2000 |
��ʹ��A | 18�� | 9�� | 3�� |
��ʹ��B | 10�� | 14�� | 1�� |
����ȫУѧ���������ȡ1�ˣ����Ƹ�ѧ���ϸ���A��B����֧����ʽ��ʹ�õĸ��ʣ�
����������ʹ��A�ͽ�ʹ��B��ѧ���и������ȡ1�ˣ���X��ʾ��2�����ϸ���֧��������1000Ԫ����������X�ķֲ��к���ѧ������
������֪�ϸ�������ѧ����֧����ʽ�ڱ���û�б仯���ִ�������ʹ��A��ѧ���У�������3�ˣ��������DZ��µ�֧��������2000Ԫ�����ݳ�������ܷ���Ϊ������ʹ��A��ѧ���б���֧��������2000Ԫ�������б仯��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���⣺��x��[��1,1]��ʹ��ʽm��x2��x�������������⣮
��1����ʵ��m��ȡֵ����M��
��2���費��ʽ��x��a��[x����2��a��]��0�Ľ⼯ΪN����NM����a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f��x���Ƕ�����R�ϵ�ż�������Ҷ������x��R����f��x+1����f��x��1������֪��x��[0��1]ʱ��f��x������![]() ��1��x����
��1��x����
��2�Ǻ���f��x����һ�����ڣ�
�ں���f��x���ڣ�1��2�����Ǽ��������ڣ�2��3��������������
�ۺ���f��x�������ֵ��1����Сֵ��0��
��x��1�Ǻ���f��x����һ���Գ��
�ݵ�x�ʣ�3��4��ʱ��f��x������![]() ��x��3.
��x��3.
����������ȷ����������_____.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �У�����
�У�����![]() �IJ�������Ϊ
�IJ�������Ϊ![]() ����
����![]() Ϊ������.������ԭ��Ϊ���㣬
Ϊ������.������ԭ��Ϊ���㣬![]() ��������Ϊ���ᣬ����������ϵ��ֱ��
��������Ϊ���ᣬ����������ϵ��ֱ��![]() ������
������![]() �����뼫�����ɵĽ�Ϊ
�����뼫�����ɵĽ�Ϊ![]() .
.
��1��������![]() ����ͨ���̼�ֱ��
����ͨ���̼�ֱ��![]() �IJ������̣�
�IJ������̣�
��2����ֱ��![]() ������
������![]() ����
����![]() ���㣬��
���㣬��![]() ����ֱ��
����ֱ��![]() ����ͨ����.
����ͨ����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������ABC��A1B1C1��ƽ��A1ACC1��ƽ��ABC����ABC��90������BAC��30����A1A��A1C��AC��E��F�ֱ���AC��A1B1���е�.
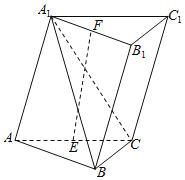
��1��֤����EF��BC��
��2����ֱ��EF��ƽ��A1BC���ɽǵ�����ֵ.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com