【题目】已知椭圆
：
的焦距为
，点
在椭圆上.
（1）求椭圆方程；
（2）设直线
：
与椭圆交于
，
两点，且直线
，
，
的斜率之和为0.
①求证：直线经过定点，并求出定点坐标；
②求
面积的最大值.
【答案】（1）
；（2）①证明见解析；②1
【解析】
(1)由条件有
，将点
代入椭圆方程结合
，可求解椭圆方程.
(2) ①设点
，
，设直线
，
，
的斜率分别为
，由条件有
，将直线方程与椭圆方程联立，将
，
代入化简可得
，得到直线过定点.
②由①利用弦长公式可求出
，再求出原点
到直线的距离，则
的面积可表示出来，从而可求其最大值.
解：（1）由题意可得，又由点在椭圆
上，故得
，
∵
，解得
，
.
∴椭圆的方程为；
（2）设点，.
联立
得
，
∴
，
化简得
①，
②，
③
设直线，，的斜率分别为
直线，，的斜率之和为0，∴
，
即
，
∴
，又
，∴.
综上可得，直线
经过定点
.
②由①知
.
∴
，
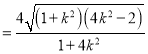原点到直线的距离
.
∴
，
∵
，
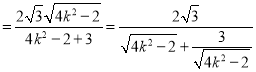当且仅当
，即
取“
”.
∴
，即面积的最大值为1.
阅读快车系列答案科目：高中数学 来源： 题型：
【题目】“割圆术”是刘徽最突出的数学成就之一，他在《九章算术注》中提出割圆术，并作为计算圆的周长，面积已经圆周率的基础，刘徽把圆内接正多边形的面积一直算到了正3072边形，并由此而求得了圆周率为3.1415和3.1416这两个近似数值，这个结果是当时世界上圆周率计算的最精确数据.如图，当分割到圆内接正六边形时，某同学利用计算机随机模拟法向圆内随机投掷点，计算得出该点落在正六边形内的频率为0.8269，那么通过该实验计算出来的圆周率近似值为（参考数据：
）
A. 3.1419B. 3.1417C. 3.1415D. 3.1413
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】（本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分
沙漏是古代的一种计时装置，它由两个形状完全相同的容器和一个狭窄的连接管道组成，开始时细沙全部在上部容器中，细沙通过连接管道全部流到下部容器所需要的时间称为该沙漏的一个沙时。如图，某沙漏由上下两个圆锥组成，圆锥的底面直径和高均为8cm，细沙全部在上部时，其高度为圆锥高度的
（细管长度忽略不计）．
（1）如果该沙漏每秒钟漏下0.02cm3的沙，则该沙漏的一个沙时为多少秒（精确到1秒）？
（2）细沙全部漏入下部后，恰好堆成个一盖住沙漏底部的圆锥形沙堆，求此锥形沙堆的高度（精确到0.1cm）．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某集团公司为了加强企业管理，树立企业形象，考虑在公司内部对迟到现象进行处罚.现在员工中随机抽取200人进行调查，当不处罚时，有80人会迟到，处罚时，得到如下数据：
处罚金额 | 50 | 100 | 150 | 200 |
迟到的人数 | 50 | 40 | 20 | 0 |
若用表中数据所得频率代替概率.
（Ⅰ）当处罚金定为100元时，员工迟到的概率会比不进行处罚时降低多少？
（Ⅱ）将选取的200人中会迟到的员工分为
，
两类：类员工在罚金不超过100元时就会改正行为；类是其他员工.现对类与类员工按分层抽样的方法抽取4人依次进行深度问卷，则前两位均为类员工的概率是多少？
查看答案和解析>>
科目：高中数学 来源： 题型：
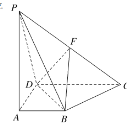
【题目】如图：四棱锥P-ABCD底面为一直角梯形，AB⊥AD,CD⊥AD,CD=2AB,PA⊥平面ABCD,F是PC中点。
（Ⅰ）求证：平面PDC⊥平面PAD;
（Ⅱ）求证：BF∥平面PAD。
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系
中，椭圆
：
过点
，
，
为椭圆的左、右焦点，离心率为
，圆
的直径为
.
（1）求椭圆及圆的方程；
（2）设直线
与圆相切于第一象限内的点
.
①若直线与椭圆有且只有一个公共点，求点的坐标；
②若直线与椭圆交于
，
两点，且
的面积为
，求直线的方程.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知圆
的圆心为
，圆内一条过点
的动弦
（与
轴不重合），过点
作
的平行线交
于点
.
（1）求出点的轨迹方程；
（2）若过点的直线
交的轨迹方程于不同两点
，
，
为坐标原点，且
，点
为椭圆上一点，求点到直线的距离的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
