
分析 (1)由f(1)=0,得到f(0)=-2,求出函数的表达式即可;
(2)得到x2-x+1=ax有解,分离a,得到a=x+$\frac{1}{x}$-1,令F(x)=x+$\frac{1}{x}$-1,x∈$(\frac{1}{2},2)$,根据函数的单调性求出即可;
(3)根据二次函数的性质得到9a2-2a+1+4ab>0,问题转化为?a∈[1,$\frac{3}{2}$),使得-4b<9a+$\frac{1}{a}$-2成立,根据基本不等式的性质求出即可.
解答 解:(1)令y=0,则f(x)-f(0)=x(x+1),
又令x=1,则f(1)-f(0)=2,
∵f(1)=0,∴f(0)=-2,
∴f(x)=x2+x-2;
(2)∵f(x)=x2+x-2=(a+2)x-3,
∴x2-x+1=ax,
∵x∈$(\frac{1}{2},2)$,∴a=x+$\frac{1}{x}$-1,
令F(x)=x+$\frac{1}{x}$-1,x∈$(\frac{1}{2},2)$,
x∈($\frac{1}{2}$,1]时,F(x)单调递减;x∈[1,2)时,F(x)单调递增,
又$F(\frac{1}{2})=F(2)=\frac{3}{2},F(1)=1$,
∴$F(x)∈[1,\frac{3}{2})$.∴$A=\left\{{a|1≤a<\frac{3}{2}}\right\}$;
(3)由a(x2+x-2)=x+b,得ax2+(a-1)x-2a-b=0有两不等实根,
依题意有△=(a-1)2+4a(2a+b)>0,
∴9a2-2a+1+4ab>0,
∴?a∈[1,$\frac{3}{2}$),使得-4b<9a+$\frac{1}{a}$-2成立,
令h(a)=9a+$\frac{1}{a}$-2,h′(a)=9-$\frac{1}{{a}^{2}}$=$\frac{(3a-1)(3a+1)}{{a}^{2}}$,
∵a∈[1,$\frac{3}{2}$)时,3a-1>0,3a+1>0,
故h′(a)>0,h(a)在[1,$\frac{3}{2}$)递增,
即h(a)=9a+$\frac{1}{a}$-2单调递增,
且a=$\frac{3}{2}$时,9a+$\frac{1}{a}$-2=$\frac{73}{6}$,
∴-4b<$\frac{73}{6}$,
∴b>-$\frac{73}{24}$.
点评 本题考查了二次函数的性质,函数的单调性问题,考查函数恒成立问题有解基本不等式的性质,是一道中档题.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x<-2或 x>1 } | B. | {x|-2<x<1 } | C. | {x|x<-1 或x>2 } | D. | {x|-1<x<2 } |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
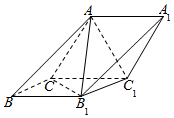 如图,在斜三棱柱ABC-A1B1C1中,侧面ACC1A1与侧面CBB1C1都是菱形,∠ACC1=∠CC1B1=60°,AC=2.
如图,在斜三棱柱ABC-A1B1C1中,侧面ACC1A1与侧面CBB1C1都是菱形,∠ACC1=∠CC1B1=60°,AC=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com