
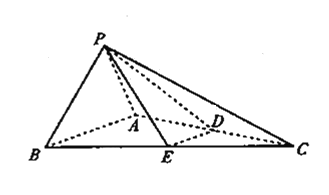
【题目】如图,在四棱锥P﹣ABCD中,PA⊥底面ABCD,△DAB≌△DCB,E为线段BD上的点,且EA=EB=ED=AB,延长CE交AD于点F.
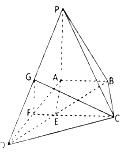
(1)若G为PD的中点,求证平面PAD⊥平面CGF;
(2)若AD=AP=6,求平面BCP与平面DCP所成锐二面角的余弦值.
【答案】(1)见解析(2)![]() .
.
【解析】
(1)推导出∠BCD=![]() ,EF⊥AD,AF=DF,GF⊥平面ABCD,GF⊥AD,从而AD⊥平面CFG,由此能证明平面PAD⊥平面CGF.
,EF⊥AD,AF=DF,GF⊥平面ABCD,GF⊥AD,从而AD⊥平面CFG,由此能证明平面PAD⊥平面CGF.
(2)以A为原点,AD为x轴,AB为y轴,AP为z轴,建立空间直角坐标系,利用向量法能求出平面BCP与平面DCP所成锐二面角的余弦值.
(1)证明:在△BCD中,EB=ED=EC=BC,∴∠BCD![]() ,
,
∵△DAB≌△DCB,∴△EAB≌△ECB,
∴∠FED=∠FEA=∠AEB![]() ,EC=EA,
,EC=EA,
∴∠FED=∠FEA,ED=EA,∴EF⊥AD,AF=DF,
∵PG=DG,∴FG∥PA,
∵PA⊥平面ABCD,∴GF⊥平面ABCD,∴GF⊥AD,
∵GF∩EF=F,∴AD⊥平面CFG,
∵AD平面PAD,∴平面PAD⊥平面CGF.
(2)解:由(1)知∠BCD![]() ,
,
∵△DAB≌△DCB,∴AB⊥AD,
∵AD=AP=6,![]() ,∴AB=2
,∴AB=2![]() ,
,
以A为原点,AD为x轴,AB为y轴,AP为z轴,建立空间直角坐标系,
P(0,0,6),B(0,2![]() ,0),C(3,3
,0),C(3,3![]() ,0),D(6,0,0),
,0),D(6,0,0),
![]() (0,2
(0,2![]() ,﹣6),
,﹣6),![]() (3,3
(3,3![]() ,﹣6),
,﹣6),![]() (6,0,﹣6),
(6,0,﹣6),
设平面BCP的法向量![]() (x,y,z),
(x,y,z),
则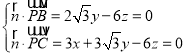 ,取x=1,得
,取x=1,得![]() (1,
(1,![]() ,﹣1),
,﹣1),
设平面DCP的法向量![]() (x,y,z),
(x,y,z),
则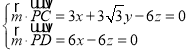 ,取x=1,得
,取x=1,得![]() (1,
(1,![]() ,1),
,1),
设平面BCP与平面DCP所成锐二面角的平面角为θ,
则cosθ .
.
∴平面BCP与平面DCP所成锐二面角的余弦值为![]() .
.



 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的一个焦点为
的一个焦点为![]() ,左右顶点分别为
,左右顶点分别为![]() .经过点
.经过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点.
两点.
(1)求椭圆方程及离心率.
(2)当直线![]() 的倾斜角为
的倾斜角为![]() 时,求线段
时,求线段![]() 的长;
的长;
(3)记![]() 的面积分别为
的面积分别为![]() 和
和![]() ,求
,求![]() 最大值.
最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD﹣A1B1C1D1中,E,F分别是棱AA1,AD上的点,且AE=EA1,AF![]() FD.
FD.
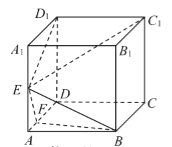
(1)求证:平面EC1D1⊥平面EFB;
(2)求二面角E﹣FB﹣A的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以坐标原点为极点,
中,以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)![]() 为曲线
为曲线![]() 上的动点,点
上的动点,点![]() 在线段
在线段![]() 上,且满足
上,且满足![]() ,求点
,求点![]() 的轨迹
的轨迹![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 的极坐标为
的极坐标为![]() ,点
,点![]() 在曲线
在曲线![]() 上,求
上,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代数学名著《九章算术》中的“蒲莞生长”是一道名题根据该问题我们改编一题:今有蒲草第一天长为三尺,莞草第一天长为一尺,以后蒲草的生长长度遂天减半,莞草的生长长度逐天加倍,现问几天后莞草的长度是蒲草的长度的两倍,以下给出了问题的四个解,其精确度最高的是(结果保留一位小数,参考数据:lg2≈0.30,lg3≈0.48)( )
A.2.6日B.3.0日C.3.6日D.4.0日
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知m,n是两条不同的直线,α,β是两个不同的平面,给出下列命题:
①若m∥n,n⊥β,mα,则α⊥β;
②若α⊥β,α∩β=m,n⊥m,则n⊥α或n⊥β;
③若m⊥α,m⊥n,nβ,则α∥β或α⊥β;
④若α∩β=m,n∥m,nα,nβ,则n∥α且n∥β;
其中正确命题的序号是( )
A.①②B.①③C.①④D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,
,
(1)求函数f(x)在x∈[﹣1,2]上的最大值和最小值;
(2)若对于任意x∈[﹣1,2]都有f(x)<m成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,![]() ,
,![]() ,
,![]() 平面PAB,D,E分别是AC,BC上的点,且
平面PAB,D,E分别是AC,BC上的点,且![]() 平面PAB.
平面PAB.
(1)求证![]() 平面PDE;
平面PDE;
(2)若D为线段AC中点,求直线PC与平面PDE所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com