
【题目】设函数f(x)=|3x﹣4|﹣|x+1|.
(1)解不等式f(x)>5;
(2)若存在实数x满足ax+a≥f(x)成立,求实数a的取值范围.
【答案】(1){x|x![]() 或x>5};(2)(﹣∞,﹣2)∪[﹣1,+∞).
或x>5};(2)(﹣∞,﹣2)∪[﹣1,+∞).
【解析】
(1)将f(x)写为分段函数的形式,然后根据f(x)>5,分别解不等式即可;
(2)直角坐标系中画出函数y=f(x)和y=ax+a的图象,利用数形结合法可得a的取值范围.
(1)f(x)=|3x﹣4|﹣|x+1| .
.
∵f(x)>5,∴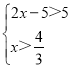 或
或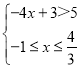 或
或![]() ,
,
∴x>5或﹣1≤x![]() 或x<﹣1,∴x
或x<﹣1,∴x![]() 或x>5,
或x>5,
∴不等式的解集为{x|x![]() 或x>5};
或x>5};
(2)由(1)知,f(x)在![]() 上单调递减,
上单调递减,
在![]() 上单调递增,且
上单调递增,且![]() .
.
在直角坐标系中画出函数y=f(x)和y=ax+a的图象,如图所示.
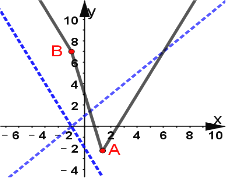
由图象可知当直线y=ax+a过A(![]() ,
,![]() )时,a=﹣1,
)时,a=﹣1,
当a=﹣2时,直线y=ax+a与直线y=﹣2x+5平行.
∵存在实数x满足ax+a≥f(x)成立,
∴由图象可知a<﹣2或a≥﹣1,
∴a的取值范围为(﹣∞,﹣2)∪[﹣1,+∞).


科目:高中数学 来源: 题型:
【题目】已知定点![]() ,圆
,圆![]() ,过R点的直线
,过R点的直线![]() 交圆于M,N两点过R点作直线
交圆于M,N两点过R点作直线![]() 交SM于Q点.
交SM于Q点.
(1)求Q点的轨迹方程;
(2)若A,B为Q的轨迹与x轴的左右交点,![]() 为该轨迹上任一动点,设直线AP,BP分别交直线l:
为该轨迹上任一动点,设直线AP,BP分别交直线l:![]() 于点M,N,判断以MN为直径的圆是否过定点。如圆过定点,则求出该定点;如不是,说明理由.
于点M,N,判断以MN为直径的圆是否过定点。如圆过定点,则求出该定点;如不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三年级有1000名学生,其中理科班学生占80%,全体理科班学生参加一次考试,考试成绩近似地服从正态分布N(72,36),若考试成绩不低于60分为及格,则此次考试成绩及格的人数约为( )
(参考数据:若Z~N(μ,σ2),则P(μ﹣σ<Z≤μ+σ)=0.6826,P(μ﹣2σ<Z<μ+2σ)=0.9544,P(μ﹣3σ<Z<μ+3σ)=0.9974)
A.778B.780C.782D.784
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PA⊥底面ABCD,△DAB≌△DCB,E为线段BD上的点,且EA=EB=ED=AB,延长CE交AD于点F.
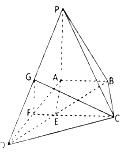
(1)若G为PD的中点,求证平面PAD⊥平面CGF;
(2)若AD=AP=6,求平面BCP与平面DCP所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】改革开放以来,人们的支付方式发生了巨大转变.近年来,移动支付已成为主要支付方式之一.为了解某校学生上个月A,B两种移动支付方式的使用情况,从全校学生中随机抽取了100人,发现样本中A,B两种支付方式都不使用的有5人,样本中仅使用A和仅使用B的学生的支付金额分布情况如下:
支付方式 | (0,1000] | (1000,2000] | 大于2000 |
仅使用A | 18人 | 9人 | 3人 |
仅使用B | 10人 | 14人 | 1人 |
(Ⅰ)从全校学生中随机抽取1人,估计该学生上个月A,B两种支付方式都使用的概率;
(Ⅱ)从样本仅使用A和仅使用B的学生中各随机抽取1人,以X表示这2人中上个月支付金额大于1000元的人数,求X的分布列和数学期望;
(Ⅲ)已知上个月样本学生的支付方式在本月没有变化.现从样本仅使用A的学生中,随机抽查3人,发现他们本月的支付金额都大于2000元.根据抽查结果,能否认为样本仅使用A的学生中本月支付金额大于2000元的人数有变化?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1,F2为椭圆E:![]() y2=1的左、右焦点,过点P(﹣2,0)的直线l与椭圆E有且只有一个交点T.
y2=1的左、右焦点,过点P(﹣2,0)的直线l与椭圆E有且只有一个交点T.
(1)求△F1TF2的面积;
(2)求证:光线![]() 被直线反射后经过F2.
被直线反射后经过F2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线![]() 的参数方程为
的参数方程为![]() ,
,![]() 为参数
为参数![]() ,在以坐标原点为极点,x轴非负半轴为极轴的极坐标系中,曲线
,在以坐标原点为极点,x轴非负半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
![]() Ⅰ
Ⅰ![]() 写出
写出![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
![]() Ⅱ
Ⅱ![]() 若
若![]() 与
与![]() 相交于A,B两点,求
相交于A,B两点,求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com