
【题目】已知定点![]() ,圆
,圆![]() ,过R点的直线
,过R点的直线![]() 交圆于M,N两点过R点作直线
交圆于M,N两点过R点作直线![]() 交SM于Q点.
交SM于Q点.
(1)求Q点的轨迹方程;
(2)若A,B为Q的轨迹与x轴的左右交点,![]() 为该轨迹上任一动点,设直线AP,BP分别交直线l:
为该轨迹上任一动点,设直线AP,BP分别交直线l:![]() 于点M,N,判断以MN为直径的圆是否过定点。如圆过定点,则求出该定点;如不是,说明理由.
于点M,N,判断以MN为直径的圆是否过定点。如圆过定点,则求出该定点;如不是,说明理由.
【答案】(1)![]() ;(2) 以MN为直径的圆经过定点
;(2) 以MN为直径的圆经过定点![]()
【解析】
(1) 利用![]() ,
,![]() ,可以推出
,可以推出![]() ,
,
根据![]() 可知: 动点
可知: 动点![]() 的轨迹是以
的轨迹是以![]() 为焦点,长轴长为4的椭圆,进而可以写出Q点的轨迹方程.
为焦点,长轴长为4的椭圆,进而可以写出Q点的轨迹方程.
(2)设![]() ,求出
,求出![]() 的坐标后,再求出
的坐标后,再求出![]() 的中点坐标,然后求出以
的中点坐标,然后求出以![]() 为直径的圆的方程,令
为直径的圆的方程,令![]() 可求得
可求得![]() 为定值,所以圆过定点.
为定值,所以圆过定点.
(1)如图:
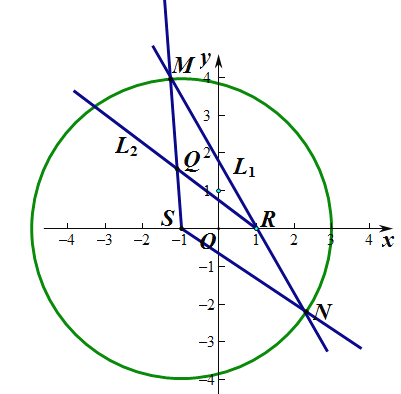
因为![]() ,
,![]() ,
,
所以![]() ,
,
所以![]() ,
,
根据椭圆的定义知:动点![]() 的轨迹是以
的轨迹是以![]() 为焦点,长轴长为4的椭圆,
为焦点,长轴长为4的椭圆,
这里![]() ,
,
所以![]() 点的轨迹方程为:
点的轨迹方程为:![]() .
.
(2)由题可知![]() ,设
,设![]() ,
,
所以![]() ,则直线
,则直线![]() 的方程为:
的方程为:![]() ,
,
令![]() ,则
,则![]() ,
,
所以![]() ,
,
因为![]() ,则直线
,则直线![]() 的方程为:
的方程为:![]() ,
,
令![]() ,则
,则![]() ,所以
,所以![]() ,
,
所以![]() 的中点坐标为
的中点坐标为![]() ,此时圆的方程为:
,此时圆的方程为:
![]() ,
,
令![]() ,得
,得![]() ,又
,又![]() ,所以
,所以![]() , 解得:
, 解得:![]() ,
,
故以MN为直径的圆经过定点![]() .
.


科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有曲池,上中周二丈,外周四丈,广一丈,下中周一丈四尺,外周二丈四尺,广五尺,深一丈,问积几何?”其意思为:“今有上下底面皆为扇形的水池,上底中周2丈,外周4丈,宽1丈;下底中周1丈4尺,外周长2丈4尺,宽5尺;深1丈.问它的容积是多少?”则该曲池的容积为( )立方尺(1丈=10尺,曲池:上下底面皆为扇形的土池,其容积公式为![]() [(2×上宽+下宽)
[(2×上宽+下宽)![]() (2×下宽+上宽)
(2×下宽+上宽)![]() ]×深)
]×深)
A.![]() B.1890C.
B.1890C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心在原点![]() ,焦点在
,焦点在![]() 轴上,离心率为
轴上,离心率为![]() 的椭圆过点
的椭圆过点![]()

(1)求椭圆的方程;
(2)设不过原点![]() 的直线
的直线![]() 与该椭圆交于
与该椭圆交于![]() 两点,满足直线
两点,满足直线![]() 的斜率依次成等比数列,求
的斜率依次成等比数列,求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率
的离心率![]() ,一个长轴顶点在直线
,一个长轴顶点在直线![]() 上,若直线
上,若直线![]() 与椭圆交于
与椭圆交于![]() ,
,![]() 两点,
两点,![]() 为坐标原点,直线
为坐标原点,直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() .
.
(1)求该椭圆的方程.
(2)若![]() ,试问
,试问![]() 的面积是否为定值?若是,求出这个定值;若不是,请说明理由.
的面积是否为定值?若是,求出这个定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的一个焦点为
的一个焦点为![]() ,左右顶点分别为
,左右顶点分别为![]() .经过点
.经过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点.
两点.
(1)求椭圆方程及离心率.
(2)当直线![]() 的倾斜角为
的倾斜角为![]() 时,求线段
时,求线段![]() 的长;
的长;
(3)记![]() 的面积分别为
的面积分别为![]() 和
和![]() ,求
,求![]() 最大值.
最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,已知直线l1的参数方程为![]() (t为参数),直线l2的参数方程为
(t为参数),直线l2的参数方程为 (t为参数),其中α∈(0,
(t为参数),其中α∈(0,![]() ),以原点O为点x轴的非负半轴为极轴,取相同的单位长度建立极坐标系,曲线C的极坐标方程为ρ﹣2sinθ=0.
),以原点O为点x轴的非负半轴为极轴,取相同的单位长度建立极坐标系,曲线C的极坐标方程为ρ﹣2sinθ=0.
(1)写出直线l1的极坐标方程和曲线C的直角坐标方程;
(2)设直线l1,l2分别与曲线C交于点A,B(非坐标原点)求|AB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为F
的右焦点为F![]() ,点B是椭圆C的短轴的一个端点,ΔOFB的面积为
,点B是椭圆C的短轴的一个端点,ΔOFB的面积为![]() ,椭圆C上的两点H、G关于原点O对称,且
,椭圆C上的两点H、G关于原点O对称,且![]() 、
、![]() 的等差中项为2
的等差中项为2
(1)求椭圆的方程;
(2)是否存在过点M(2,1)的直线![]() 与椭圆C交于不同的两点P、Q,且使得
与椭圆C交于不同的两点P、Q,且使得![]() 成立?若存在,试求出直线
成立?若存在,试求出直线![]() 的方程;若不存在,请说明理由
的方程;若不存在,请说明理由
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】贵阳市交管部门于2018年4月对贵阳市长期执行的“两限”政策进行了调整,调整后贵阳市贵A普客小汽车拥有和外地牌照汽车一样的驶入一环开四停四的权利,为统计开放政策实施后贵阳市一环内城区的交通流量状况,市交管部门抽取了某月30天内的日均汽车流量与实际容纳量进行对比,比值记为![]() ,若该比值不超过1称为“畅通”,否则称为“拥堵”,如图所示的程序框图实现的功能是( )
,若该比值不超过1称为“畅通”,否则称为“拥堵”,如图所示的程序框图实现的功能是( )
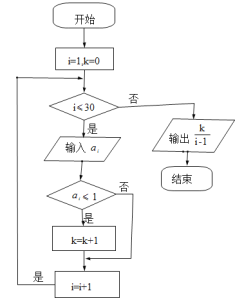
A.求30天内交通的畅通率B.求30天内交通的拥堵率
C.求30天内交通的畅通天数D.求30天内交通的拥堵天数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com