练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，多面体中，平面平面，，四边形为平行四边形.

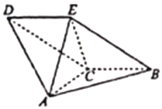
    （1）证明：；

    （2）若，求二面角的余弦值.

    【答案】（1）证明见解析（2）

    【解析】

    （1）先通过平面平面得到，再结合，可得平面，进而可得结论；

    （2）取的中点，的中点，连接，，以点为坐标原点，分别以，，为轴，轴，轴建立空间直角坐标系，求出平面的一个法向量以及平面的一个法向量，求这两个法向量的夹角即可得结果.

    解：（1）因为平面平面，交线为，又，

    所以平面，，又，，

    则平面，平面，

    所以，；

    （2）取的中点，的中点，连接，，则平面，平面；

    以点为坐标原点，分别以，，为轴，轴，轴建立空间直角坐标系如图所示，

    　　　　

    已知，则，，

    ，，，，

    则，，

    设平面的一个法向量，

    由得令，则，，

    即；

    平面的一个法向量为；

    .

    所以二面角的余弦值为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知中心在原点，焦点在轴上，离心率为的椭圆过点

    （1）求椭圆的方程；

    （2）设不过原点的直线与该椭圆交于两点，满足直线的斜率依次成等比数列，求面积的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的右焦点为F，点B是椭圆C的短轴的一个端点，ΔOFB的面积为，椭圆C上的两点H、G关于原点O对称，且、的等差中项为2

    （1）求椭圆的方程；

    （2）是否存在过点M（2，1）的直线与椭圆C交于不同的两点P、Q，且使得成立？若存在，试求出直线的方程；若不存在，请说明理由

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】贵阳市交管部门于2018年4月对贵阳市长期执行的“两限”政策进行了调整，调整后贵阳市贵A普客小汽车拥有和外地牌照汽车一样的驶入一环开四停四的权利，为统计开放政策实施后贵阳市一环内城区的交通流量状况，市交管部门抽取了某月30天内的日均汽车流量与实际容纳量进行对比，比值记为，若该比值不超过1称为“畅通”，否则称为“拥堵”，如图所示的程序框图实现的功能是（ ）

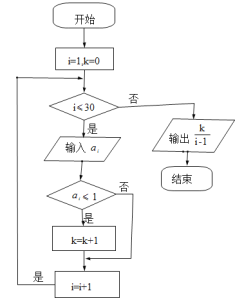
    A.求30天内交通的畅通率B.求30天内交通的拥堵率

    C.求30天内交通的畅通天数D.求30天内交通的拥堵天数

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在正方体ABCD﹣A1B1C1D1中，E，F分别是棱AA1，AD上的点，且AE=EA1，AFFD.

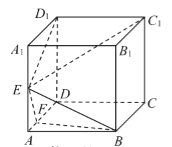
    （1）求证：平面EC1D1⊥平面EFB；

    （2）求二面角E﹣FB﹣A的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】

    已知函数f（x）=，其中a>0.

    （Ⅰ）若a=1，求曲线y=f（x）在点（2，f（2））处的切线方程；

    （Ⅱ）若在区间上，f（x）>0恒成立，求a的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系中，以坐标原点为极点，轴正半轴为极轴建立极坐标系，曲线的极坐标方程为．

    （1）为曲线上的动点，点在线段上，且满足，求点的轨迹的直角坐标方程；

    （2）设点的极坐标为，点在曲线上，求面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数f（x）＝|3x﹣4|﹣|x+1|．

    （1）解不等式f（x）＞5；

    （2）若存在实数x满足ax+a≥f（x）成立，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】椭圆将圆的圆周分为四等份，且椭圆的离心率为.

    （1）求椭圆的方程；

    （2）若直线与椭圆交于不同的两点，且的中点为，线段的垂直平分线为，直线与轴交于点，求的取值范围.

    查看答案和解析>>

    同步练习册答案