
分析 运用定积分公式,求得n=6,再求二项式的通项公式,化简整理,解方程可得r,进而得到所求系数.
解答 解:n=9$\int_{-1}^1{x^2}$dx=9×$\frac{1}{3}$x3|${\;}_{-1}^{1}$=9×$\frac{2}{3}$=6,
二项式(x-$\frac{2}{x}$)6的展开式的通项公式为
Tr+1=${C}_{6}^{r}$x6-r(-$\frac{2}{x}$)r=${C}_{6}^{r}$x6-2r(-2)r,r=0,1,2,…,6,
令6-2r=2,解得r=2,
则x2的系数是${C}_{6}^{2}$(-2)2=60.
故答案为:60.
点评 本题考查二项式定理的运用:求指定项的系数,同时考查定积分的运算,属于基础题.


 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | -3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
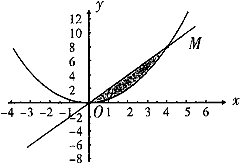 设曲线x2=2y与过原点的直线相交于点M,若直线OM的倾斜角为θ,则线段OM与曲线围成的封闭图形的面积S(θ)的图象大致是( )
设曲线x2=2y与过原点的直线相交于点M,若直线OM的倾斜角为θ,则线段OM与曲线围成的封闭图形的面积S(θ)的图象大致是( )| A. | 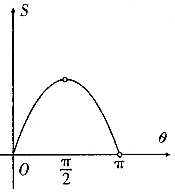 | B. | 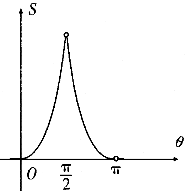 | ||
| C. | 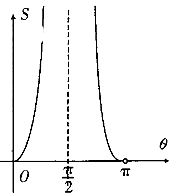 | D. | 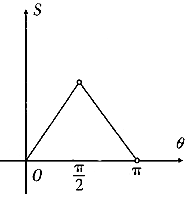 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com