
【题目】设△ABC的内角A、B、C的对边分别为a、b、c,且满足sinA+sinB=[cosA﹣cos(π﹣B)]sinC.
(1)试判断△ABC的形状,并说明理由;
(2)若a+b+c=1+ ![]() ,试求△ABC面积的最大值.
,试求△ABC面积的最大值.
【答案】
(1)解:∵sinA+sinB=[cosA﹣cos(π﹣B)]sinC,
∴sinA+sinB=(cosA+cosB)sinC,
由正弦定理和余弦定理得,
a+b=( ![]() +
+ ![]() )c,
)c,
化简得,2a2b+2ab2=ab2+ac2﹣a3+ba2+bc2﹣b3
a2b+ab2=ac2﹣a3+bc2﹣b3,
(a+b)(a2+b2﹣c2)=0,
又a+b>0,∴a2+b2﹣c2=0,即a2+b2=c2,
∴△ABC为直角三角形,且∠C=90°
(2)解:∵a+b+c=1+ ![]() ,a2+b2=c2,
,a2+b2=c2,
∴1+ ![]() =a+b+
=a+b+ ![]() ≥2
≥2 ![]() +
+ ![]() =(2+
=(2+ ![]() )
) ![]()
当且仅当a=b时上式等号成立,则 ![]() ≤
≤ ![]() =
= ![]() ,
,
∴S△ABC= ![]() ab≤
ab≤ ![]() ×
× ![]() =
= ![]() ,
,
即△ABC面积的最大值为 ![]()
【解析】(1)由诱导公式、正弦定理和余弦定理化简已知的式子,化简后由边的关系判断出三角形的形状;(2)由(1)和条件化简后,由基本不等式化简求出 ![]() 的范围,表示三角形的面积,即可求出答案.
的范围,表示三角形的面积,即可求出答案.
【考点精析】利用正弦定理的定义和余弦定理的定义对题目进行判断即可得到答案,需要熟知正弦定理:![]() ;余弦定理:
;余弦定理:![]() ;
;![]() ;
;![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() ,(
,(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 是曲线
是曲线![]() 上的一个动点,求它到直线
上的一个动点,求它到直线![]() 的距离
的距离![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】双曲线E: ![]() =1(a>0,b>0)的左、右焦点分别为F1、F2 , P是E坐支上一点,且|PF1|=|F1F2|,直线PF2与圆x2+y2=a2相切,则E的离心率为 .
=1(a>0,b>0)的左、右焦点分别为F1、F2 , P是E坐支上一点,且|PF1|=|F1F2|,直线PF2与圆x2+y2=a2相切,则E的离心率为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 两个变量的相关关系一定是线性相关
B. 两个随机变量的线性相关线越强,则相关系数的绝对值就越接近于0
C. 在回归直线方程![]() 中,当解释变量
中,当解释变量![]() 每增加1个单位时,预报变量
每增加1个单位时,预报变量![]() 平均增加1个单位
平均增加1个单位
D. 对分类变量![]() 与
与![]() ,随机变量
,随机变量![]() 的观测值
的观测值![]() 越大,则判断“
越大,则判断“![]() 与
与![]() 有关系”的把握程度越大
有关系”的把握程度越大
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种商品在![]() 天内每件的销售价格
天内每件的销售价格![]() (元)与时间
(元)与时间![]() (
(![]() )(天)的函数关系满足函数
)(天)的函数关系满足函数 ,该商品在
,该商品在![]() 天内日销售量
天内日销售量![]() (件)与时间
(件)与时间![]() (
(![]() )(天)之间满足一次函数关系如下表:
)(天)之间满足一次函数关系如下表:
第 |
|
|
|
|
|
|
|
|
|
(1)根据表中提供的数据,确定日销售量![]() 与时间
与时间![]() 的一次函数关系式;
的一次函数关系式;
(2)求该商品的日销售金额的最大值并指出日销售金额最大的一天是![]() 天中的第几天,(日销售金额
天中的第几天,(日销售金额![]() 每件的销售价格
每件的销售价格![]() 日销售量)
日销售量)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() =1(a>b>0)上的点到右焦点F的最小距离是
=1(a>b>0)上的点到右焦点F的最小距离是 ![]() ﹣1,F到上顶点的距离为
﹣1,F到上顶点的距离为 ![]() ,点C(m,0)是线段OF上的一个动点.
,点C(m,0)是线段OF上的一个动点.
(1)求椭圆的方程;
(2)是否存在过点F且与x轴不垂直的直线l与椭圆交于A、B两点,使得( ![]() +
+ ![]() )⊥
)⊥ ![]() ,并说明理由.
,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某服装批发市场1-5月份的服装销售量![]() 与利润
与利润![]() 的统计数据如下表:
的统计数据如下表:
月份 | 1 | 2 | 3 | 4 | 5 |
销售量 | 3 | 6 | 4 | 7 | 8 |
利润 | 19 | 34 | 26 | 41 | 46 |
(1)从这五个月的利润中任选2个,分别记为![]() ,
, ![]() ,求事件“
,求事件“![]() ,
, ![]() 均不小于30”的概率;
均不小于30”的概率;
(2)已知销售量![]() 与利润
与利润![]() 大致满足线性相关关系,请根据前4个月的数据,求出
大致满足线性相关关系,请根据前4个月的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)若由线性回归方程得到的利润的估计数据与真实数据的误差不超过2万元,则认为得到的利润的估计数据是理想的.请用表格中第5个月的数据检验由(2)中回归方程所得的第5个月的利润的估计数据是否理想.参考公式:  .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
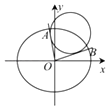
【题目】如图所示,已知椭圆C: ![]() +
+ ![]() =1(a>b>0)的焦距为2,直线y=x被椭圆C截得的弦长为
=1(a>b>0)的焦距为2,直线y=x被椭圆C截得的弦长为 ![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设点M(x0 , y0)是椭圆C上的动点,过原点O引两条射线l1 , l2与圆M:(x﹣x0)2+(y﹣y0)2= ![]() 分别相切,且l1 , l2的斜率k1 , k2存在.
分别相切,且l1 , l2的斜率k1 , k2存在.
①试问k1k2是否定值?若是,求出该定值,若不是,说明理由;
②若射线l1 , l2与椭圆C分别交于点A,B,求|OA||OB|的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com