
【题目】某服装批发市场1-5月份的服装销售量![]() 与利润
与利润![]() 的统计数据如下表:
的统计数据如下表:
月份 | 1 | 2 | 3 | 4 | 5 |
销售量 | 3 | 6 | 4 | 7 | 8 |
利润 | 19 | 34 | 26 | 41 | 46 |
(1)从这五个月的利润中任选2个,分别记为![]() ,
, ![]() ,求事件“
,求事件“![]() ,
, ![]() 均不小于30”的概率;
均不小于30”的概率;
(2)已知销售量![]() 与利润
与利润![]() 大致满足线性相关关系,请根据前4个月的数据,求出
大致满足线性相关关系,请根据前4个月的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)若由线性回归方程得到的利润的估计数据与真实数据的误差不超过2万元,则认为得到的利润的估计数据是理想的.请用表格中第5个月的数据检验由(2)中回归方程所得的第5个月的利润的估计数据是否理想.参考公式:  .
.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)见解析.
;(3)见解析.
【解析】试题分析:(1)列出基本事件,和事件A所包含的基本事件,由古典概型可求。(2)由公式依次算出![]() 。(3)由(2)得线性回归方程为
。(3)由(2)得线性回归方程为![]() ,代入
,代入![]() 进行误差分析。
进行误差分析。
试题解析:(1)所有的基本事件为(19,34), (19,26), (19,41),(19,46),(34,26) ,(34,41) ,(34,46),
(26,41),(26,46),(41,46)共10个.记“m,n均不小于30”为事件A,则事件A包含的基本事件为(34,41) ,(34,46), (41,46),共3个.所以![]() .
.
(2)由前4个月的数据可得, ![]()
![]() .
.
所以 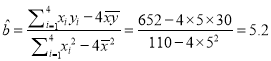 ,
,
![]() ,所以线性回归方程为
,所以线性回归方程为![]()
(3)由题意得,当![]() 时,
时, ![]() ,
, ![]() ; 所以利用(2)中的回归
; 所以利用(2)中的回归
方程所得的第5个月的利润估计数据是理想的.


科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为ρsin(θ+ ![]() )=
)= ![]() .圆O的参数方程为
.圆O的参数方程为  (θ为参数,r>0).
(θ为参数,r>0).
(Ⅰ)求圆O的圆心的极坐标(ρ≥0,0≤θ<2π );
(Ⅱ)当r为何值时,圆O上的点到直线l的最大距离为2+ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax3+3x2+1,若至少存在两个实数m,使得f(﹣m),f(1)、f(m+2)成等差数列,则过坐标原点作曲线y=f(x)的切线可以作( )
A.3条
B.2条
C.1条
D.0条
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(cosx,sinx),
=(cosx,sinx), ![]() =(3,﹣
=(3,﹣ ![]() ),x∈[0,π].
),x∈[0,π].
(1)若 ![]() ∥
∥ ![]() ,求x的值;
,求x的值;
(2)记f(x)= ![]() ,求f(x)的最大值和最小值以及对应的x的值.
,求f(x)的最大值和最小值以及对应的x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两人玩猜数字游戏,先由甲心中任想一个数字记为![]() ,再由乙猜甲刚才想的数字,把乙猜的数字记为
,再由乙猜甲刚才想的数字,把乙猜的数字记为![]() ,且
,且![]() 、
、![]() .若
.若![]() ,则称甲乙“心有灵犀”.现任意找两人玩这个游戏,则二人“心有灵犀”的概率为__________.
,则称甲乙“心有灵犀”.现任意找两人玩这个游戏,则二人“心有灵犀”的概率为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空气质量问题,全民关注,有需求就有研究,某科研团队根据工地常用高压水枪除尘原理,制造了雾霾神器﹣﹣﹣雾炮,虽然雾炮不能彻底解决问题,但是能在一定程度上起到防霾、降尘的作用,经过测试得到雾炮降尘率的频率分布直方图:
若降尘率达到18%以上,则认定雾炮除尘有效.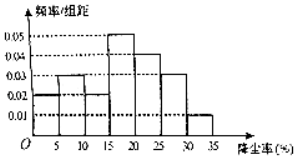
(1)根据以上数据估计雾炮除尘有效的概率;
(2)现把A市规划成三个区域,每个区域投放3台雾炮进行除尘(雾炮之间工作互不影响),若在一个区域内的3台雾炮降尘率都低于18%,则需对该区域后期追加投入20万元继续进行治理,求后期投入费用的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn , 且2Sn=(n+2)an﹣1(n∈N*).
(1)求a1的值;
(2)求数列{an}的通项公式;
(3)设Tn= ![]() ,求证:Tn<
,求证:Tn< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0)左、右焦点分别为F1 , F2 , A(2,0)是椭圆的右顶点,过F2且垂直于x轴的直线交椭圆于P,Q两点,且|PQ|=3;
(a>b>0)左、右焦点分别为F1 , F2 , A(2,0)是椭圆的右顶点,过F2且垂直于x轴的直线交椭圆于P,Q两点,且|PQ|=3;
(1)求椭圆的方程;
(2)若直线l与椭圆交于两点M,N(M,N不同于点A),若 ![]()
![]() =0,
=0, ![]() =
= ![]() ;
;
①求证:直线l过定点;并求出定点坐标;
②求直线AT的斜率的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com