
| A. | 直角三角形 | B. | 等腰三角形 | ||
| C. | 等腰或直角三角形 | D. | 等边三角形 |
分析 由正弦定理将角的关系转化为边的关系,⇒(a2-b2)(a2+b2-c2)=0⇒a2=b2或a2+b2-c2=0.
解答 解:由正弦定理$\frac{asinA}{{{a^2}+{c^2}-{b^2}}}=\frac{bsinB}{{{b^2}+{c^2}-{a^2}}}$可变为$\frac{{a}^{2}}{{a}^{2}+{c}^{2}-{b}^{2}}=\frac{{b}^{2}}{{b}^{2}+{c}^{2}-{a}^{2}}$
⇒$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{{a}^{2}}=\frac{{b}^{2}+{c}^{2}-{a}^{2}}{{b}^{2}}$⇒$\frac{{c}^{2}-{b}^{2}}{{a}^{2}}=\frac{{c}^{2}-{a}^{2}}{{b}^{2}}$
⇒b2(c2-b2)=a2(c2-a2)⇒(a2-b2)(a2+b2-c2)=0
⇒a2=b2或a2+b2-c2=0.
∴△ABC等腰或直角三角形,
故选:C
点评 本题考查余弦定理的应用,边角关系的转换,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{n}>\frac{1}{m}$ | B. | |n|>|m| | C. | $\frac{n}{m}+\frac{m}{n}>2$ | D. | m+n>mn |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2$\sqrt{3}$ | C. | 2 | D. | -3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 120 | B. | 80 | C. | 15 | D. | 150 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
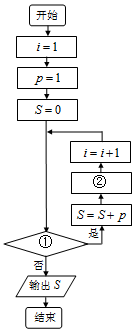 给出50个数,1,2,4,7,11,…,其规律是:第1个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3,…,以此类推.要求计算这50个数的和.
给出50个数,1,2,4,7,11,…,其规律是:第1个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3,…,以此类推.要求计算这50个数的和.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若x2≥1,则x≥1,或x≤-1 | B. | 若-1<x<1,则x2<1 | ||
| C. | 若x≥1或x≤-1,则x2≥1 | D. | 若x>1或x<-1,则x2>1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,设椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点分别为F1,F2,离心率为e=$\frac{\sqrt{2}}{2}$,右准线L上两动点M,N,F2为△F1MN的垂心.
如图,设椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)的左右焦点分别为F1,F2,离心率为e=$\frac{\sqrt{2}}{2}$,右准线L上两动点M,N,F2为△F1MN的垂心.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com