
| a |
| b |
| OA |
| a |
| OB |
| b |
| OC |
| a |
| b |
| x |
| p |
| y |
| q |
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:
| AB |
| BC |
| CD |
| DA |
| 0 |
| a |
| b |
| c |
| a |
| b |
| b |
| c |
| c |
| a |
| a |
| b |
| c |
| a |
| b |
| c |
| OP |
| OA |
| OB |
| OC |
| A、3 | B、2 | C、1 | D、0 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b, |
| c |
| a+b |
| a-b |
| c |
| a |
| b |
| a |
| b |
| OP |
| OA |
| OB |
| OC |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
查看答案和解析>>
科目:高中数学 来源: 题型:
| AB |
| BA |
| AB |
| BC |
| CD |
| DA |
| 0 |
| a |
| b |
| a |
| b |
| AB |
| AB |
| OA |
| OB |
| OC |
| OD |
查看答案和解析>>
科目:高中数学 来源: 题型:
在下列四个命题中
①已知A、B、C、D是空间的任意四点,则![]() .
.
②若{![]() }为空间的一组基底,则{
}为空间的一组基底,则{![]() }也构成空间的一组基底.
}也构成空间的一组基底.
③![]() .
.
④对于空间的任意一点O和不共线的三点A、B、C,若![]() (其中
(其中![]() ),则P、A、B、C四点共面.
),则P、A、B、C四点共面.
其中正确的个数是 ( )
A.3 A.2 C.1 D.0
查看答案和解析>>
科目:高中数学 来源:2013届河北省高二上学期第二次月考理科数学试卷 题型:填空题
下面关于向量的结论中,
(1) ;(2)
;(2)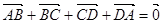 ;(3)若
;(3)若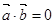 ,则
,则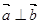 ;
;
(4)若向量 平移后,起点和终点的发生变化,所以
平移后,起点和终点的发生变化,所以 也发生变化;
也发生变化;
(5)已知A、B、C、D四点满足任三点不共线,但四点共面,O是平面ABCD外任一点,且 其中正确的序号为
其中正确的序号为
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com