练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知变量x，y满足约束条件，则z=2x+y的最大值为        ．


    8

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    请阅读下列材料：若两个正实数a1，a2满足a＋a＝1，那么a1＋a2≤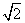.证明：构造函数f(x)＝(x－a1)2＋(x－a2)2＝2x2－2(a1＋a2)x＋1，因为对一切实数x，恒有f(x)≥0，所以Δ≤0，从而得4(a1＋a2)2－8≤0，所以a1＋a2≤.

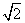    根据上述证明方法，若n个正实数满足a＋a＋…＋a＝1时，你能得到的结论为________．(不必证明)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某产品在某零售摊位上的零售价x(元)与每天的销售量y(个)统计如下表：

    x

    16

    17

    18

    19

    y

    50

    41

    34

    31

    据上表可得回归直线方程＝bx＋a中的b＝－4，据此模型预计零售价定为15元时，销售量为(　　)

    A．48  B．49  C．50  D．51

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    椭圆上有一点P到左焦点的距离是4，则点p到右焦点的距离是（   ）

       A.3                B.、4              C.5             D.6

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设 且,则的最小值为       （   ）

       A．12            B．15               C．16               D．-16

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在中，是三角形的三内角，是三内角对应的三边，已知．

    （1）求角的大小；

     (2) 若＝，求中周长和面积的最大值

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    k棱柱有f(k)个对角面，则k＋1棱柱的对角面个数f(k＋1)为(　　)

    A．f(k)＋k－1　   B．f(k)＋k＋1  C．f(k)＋k       D．f(k)＋k－2

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝x2＋ax＋3，g(x)＝(6＋a)·2x－1.

    (1)若f(1)＝f(3)，求实数a的值；

    (2)在(1)的条件下，判断函数F(x)＝的单调性，并给出证明；

    (3)当x∈[－2,2]时，f(x)≥a(a∉(－4,4))恒成立，求实数a的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若一个球的体积为，则它的表面积为　

    查看答案和解析>>

    同步练习册答案