
设椭圆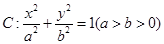 过点
过点 (
(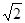 ,1),且左焦点为
,1),且左焦点为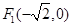 .
.
(1)求椭圆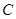 的方程;
的方程;
(2)判断是否存在经过定点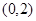 的直线
的直线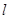 与椭圆
与椭圆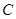 交于
交于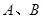 两点并且满足
两点并且满足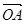 ·
·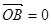 ,若存在求出直线
,若存在求出直线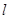 的方程,不存在说明理由.
的方程,不存在说明理由.
 灵星计算小达人系列答案
灵星计算小达人系列答案科目:高中数学 来源:2013届广东省高二第七学段文科数学试卷(解析版) 题型:解答题
(本小题满分14分)设椭圆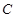 :
:  过点(0,4),离心率为
过点(0,4),离心率为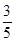 .
.
(1)求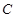 的方程;
的方程;
(2)求过点(3,0)且斜率为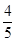 的直线被
的直线被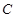 所截线段的中点坐标.
所截线段的中点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 过点M(
过点M( ,1),且左焦点为
,1),且左焦点为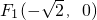 .
. •
•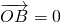 ,若存在求出直线l的方程,不存在说明理由.
,若存在求出直线l的方程,不存在说明理由.查看答案和解析>>
科目:高中数学 来源:福建省期末题 题型:解答题
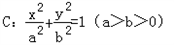 过点M(
过点M(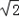 ,1),且左焦点为
,1),且左焦点为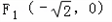 .
.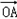 ·
·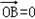 ,若存在求出直线l的方程,不存在说明理由.
,若存在求出直线l的方程,不存在说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com