
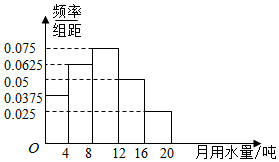
 水是最常见的物质之一,是包括人类在内所有生命生存的重要资源,也是生物体最重要的组成部分,为了推动对水资源迸行综合性统筹规划和管理,加强水资源保护,解决日益严峻的淡水缺乏问题,开展广泛的宣传以提高公众对开发和保护水资源的认识,中国水利部确定每年的3月22日至28日为“中国水周”,以提倡市民节约用水.某市统计局凋查了该市众多家庭的用水量情况,绘制了月用水量的频率分布直方图,如图所示.将月用水量落人各组的频率视为概率,并假设每天的用水量相互独立.
水是最常见的物质之一,是包括人类在内所有生命生存的重要资源,也是生物体最重要的组成部分,为了推动对水资源迸行综合性统筹规划和管理,加强水资源保护,解决日益严峻的淡水缺乏问题,开展广泛的宣传以提高公众对开发和保护水资源的认识,中国水利部确定每年的3月22日至28日为“中国水周”,以提倡市民节约用水.某市统计局凋查了该市众多家庭的用水量情况,绘制了月用水量的频率分布直方图,如图所示.将月用水量落人各组的频率视为概率,并假设每天的用水量相互独立.分析 (Ⅰ)由频率分布直方图估计该地家庭的平均用水量.
(Ⅱ)频率分布直方图得用水量不低于12吨的频率和月用水量低于4吨的频率,由此能求出有连续2个月的月用水量都不低于12吨且另1个月的用水量低于4吨的概率.
(Ⅲ)由题意X的可能取值为0,1,2,3,X~B(3,0.3),由此能求出X的分布列和EX.
解答 解:(Ⅰ)由频率分布直方图估计该地家庭的平均用水量为:
$\overline{x}$=2×0.0375×4+6×0.0625×4+10×0.075×4+14×0.05×4+18×0.025×4=9.4(吨).
(Ⅱ)频率分布直方图得用水量不低于12吨的频率为(0.05+0.025)×4=0.3,月用水量低于4吨的频率为0.0375×4=0.15,
∴有连续2个月的月用水量都不低于12吨且另1个月的用水量低于4吨的概率:
p=0.3×0.3×0.15+0.3×0.3×0.15=0.027.
(Ⅲ)由题意X的可能取值为0,1,2,3,X~B(3,0.3),
P(X=0)=${C}_{3}^{0}(0.7)^{3}$=0.343,
P(X=1)=${C}_{3}^{1}(0.3)(0.7)^{2}$=0.441,
P(X=2)=${C}_{3}^{2}(0.3)^{2}(0.7)$=0.189,
P(X=3)=${C}_{3}^{3}(0.3)^{3}$=0.027,
∴X的分布列为:
| X | 0 | 1 | 2 | 3 |
| P | 0.343 | 0.441 | 0.189 | 0.027 |
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意二项分布的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题:若x=3,则x2-2x-3=0的否命题是:若x≠3,则x2-2x-3≠0 | |
| B. | 命题:?x∈R,使得x2-1<0的否定是:?x∈R,均有x2-1<0 | |
| C. | 命题:存在四边相等的四边形不是正方形,该命题是假命题 | |
| D. | 命题:cosx=cosy,则x=y的逆否命题是真命题 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com