
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
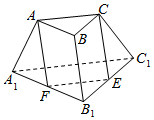 在三棱台ABC-A1B1C1中,A1B1=2AB,点E、F分别是棱B1C1、A1B1的中点,则在三棱台的各棱所在的直线中,与平面ACEF平行的有A1C1、BB1.
在三棱台ABC-A1B1C1中,A1B1=2AB,点E、F分别是棱B1C1、A1B1的中点,则在三棱台的各棱所在的直线中,与平面ACEF平行的有A1C1、BB1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4031 | B. | 4033 | C. | 4034 | D. | 4032 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ③④ | B. | ②③ | C. | ①④ | D. | ①②③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
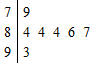 我校为了丰富同学们的课余生活,特举办了一次挑战主持人大赛,如图是七位评委为某选手打出的分数的茎叶图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )
我校为了丰富同学们的课余生活,特举办了一次挑战主持人大赛,如图是七位评委为某选手打出的分数的茎叶图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )| A. | 4;4 | B. | 5;1.6 | C. | 84;4 | D. | 85;1.6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
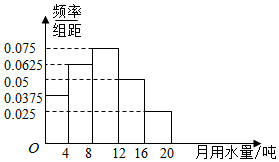 水是最常见的物质之一,是包括人类在内所有生命生存的重要资源,也是生物体最重要的组成部分,为了推动对水资源迸行综合性统筹规划和管理,加强水资源保护,解决日益严峻的淡水缺乏问题,开展广泛的宣传以提高公众对开发和保护水资源的认识,中国水利部确定每年的3月22日至28日为“中国水周”,以提倡市民节约用水.某市统计局凋查了该市众多家庭的用水量情况,绘制了月用水量的频率分布直方图,如图所示.将月用水量落人各组的频率视为概率,并假设每天的用水量相互独立.
水是最常见的物质之一,是包括人类在内所有生命生存的重要资源,也是生物体最重要的组成部分,为了推动对水资源迸行综合性统筹规划和管理,加强水资源保护,解决日益严峻的淡水缺乏问题,开展广泛的宣传以提高公众对开发和保护水资源的认识,中国水利部确定每年的3月22日至28日为“中国水周”,以提倡市民节约用水.某市统计局凋查了该市众多家庭的用水量情况,绘制了月用水量的频率分布直方图,如图所示.将月用水量落人各组的频率视为概率,并假设每天的用水量相互独立.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com