在等差数列{an}中,已知a4=-3,且a1-2、a3、a5成等比数列,n∈N*
(Ⅰ)求数列{an}的公差d;
(Ⅱ)设数列{an}的前n项和为Sn,求Sn的最值.
解:(Ⅰ)由题意可得 a
1=-3-3d,a
3=-3-d,a
5=-3+d.
∵
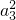
=(a
1-2 )a
5 ,
∴(-3-d)
2=(-3-3d-2 )(-3+3d ).
解得 d=1,或d=-

.
(Ⅱ)①当d=1 时,a
n=-3+(n-4)d=n-7,故此数列为递增数列.
令 a
n=0 可得 n=7,故当n=6 或n=7时,S
n 取得最小值为-21,且S
n 不存在最大值.
②当 d=-

时,a
n=-3+(n-4)(-

)=-

n+3,故此数列为递减数列.
令a
n=0 可得 n=2,故当n=1 或n=2时,S
n 取得最大值为

,且S
n 不存在最小值.
分析:(Ⅰ)由题意可得a
1=-3-3d,a
3=-3-d,a
5=-3+d,(-3-3d)
2=(-3-3d-2 )(-3+3d ),解方程求得d的值.
(Ⅱ)根据d的值求出数列的通项公式,由数列的通项公式判断数列的单调性,从而求出它的最值.
点评:本题主要考查等比数列的定义和性质,等差数列的通项公式,以及数列的函数特性,属于中档题.

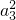 =(a1-2 )a5 ,
=(a1-2 )a5 , .
. 时,an=-3+(n-4)(-
时,an=-3+(n-4)(- )=-
)=- n+3,故此数列为递减数列.
n+3,故此数列为递减数列. ,且Sn 不存在最小值.
,且Sn 不存在最小值.

 名校课堂系列答案
名校课堂系列答案