
分析 (Ⅰ)由题意可得$\frac{1}{a}$+$\frac{4}{b}$=($\frac{1}{a}$+$\frac{4}{b}$)(a+b)=5+$\frac{b}{a}$+$\frac{4a}{b}$,由基本不等式可得;
(Ⅱ)问题转化为|2x-1|-|x+1|≤9,去绝对值化为不等式组,解不等式组可得.
解答 解:(Ⅰ)∵a+b=1,a>0,b>0,
∴$\frac{1}{a}$+$\frac{4}{b}$=($\frac{1}{a}$+$\frac{4}{b}$)(a+b)=5+$\frac{b}{a}$+$\frac{4a}{b}$
≥5+2$\sqrt{\frac{b}{a}•\frac{4a}{b}}$=9,
当且仅当$\frac{b}{a}$=$\frac{4a}{b}$即a=$\frac{1}{3}$且b=$\frac{2}{3}$时取等号,
∴$\frac{1}{a}$+$\frac{4}{b}$的最小值为9;
(Ⅱ)若不等式$\frac{1}{a}$+$\frac{4}{b}$≥|2x-1|-|x+1|对任意a,b恒成立,
则需|2x-1|-|x+1|≤9,可转化为$\left\{\begin{array}{l}{x≤-1}\\{-(2x-1)+(x+1)≤9}\end{array}\right.$,
或$\left\{\begin{array}{l}{x≥\frac{1}{2}}\\{2x-1-(x+1)≤9}\end{array}\right.$或$\left\{\begin{array}{l}{-1<x<\frac{1}{2}}\\{-(2x-1)-(x+1)≤9}\end{array}\right.$,
分别解不等式组可得-7≤x≤-1,$\frac{1}{2}$≤x≤11,-1<x<$\frac{1}{2}$
综合可得x的取值范围为[-7,11]
点评 本题考查基本不等式求最值,涉及恒成立和绝对值不等式,属中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
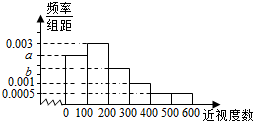 某普通高中为了了解学生的视力状况,随机抽查了100名高二年级学生和100名高三年级学生,对这些学生配戴眼镜的度数(简称:近视度数)进行统计,得到高二学生的频数分布表和高三学生频率分布直方图如下:
某普通高中为了了解学生的视力状况,随机抽查了100名高二年级学生和100名高三年级学生,对这些学生配戴眼镜的度数(简称:近视度数)进行统计,得到高二学生的频数分布表和高三学生频率分布直方图如下:| 近视度数 | 0-100 | 100-200 | 200-300 | 300-400 | 400以上 |
| 学生频数 | 30 | 40 | 20 | 10 | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com