
| 1 | 2 | 3 | -7 |
| -2 | 1 | 1 |
| a | a2-1 | -a | -a2 |
| 2-a | 1-a2 | a-2 | a2 |
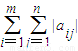 ,可见其增加的趋势必在有限次之后终止,终止之时必然所有的行和与所有的列和均为非负整数,故结论成立.
,可见其增加的趋势必在有限次之后终止,终止之时必然所有的行和与所有的列和均为非负整数,故结论成立.| 1 | 2 | 3 | -7 |
| -2 | 1 | 1 |
| 1 | 2 | 3 | 7 |
| -2 | 1 | -1 |
| 1 | 2 | 3 | 7 |
| 2 | -1 | 1 |
| 1 | 2 | 3 | -7 |
| -2 | 1 | 1 |
| 1 | 2 | 3 | 7 |
| 2 | -1 | -1 |
| 1 | 2 | 3 | 7 |
| 2 | -1 | 1 |
| 1 | 2 | 3 | -7 |
| -2 | 1 | 1 |
| -1 | 2 | 3 | 7 |
| 2 | 1 | -1 |
| -1 | 2 | 3 | 7 |
| 2 | 1 | -1 |
| a | a2-1 | a | -a2 |
| 2-a | 1-a2 | -a+2 | a2 |
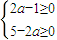 ,解得a=1,a=2.…(6分)
,解得a=1,a=2.…(6分)| -a | -a2+1 | a | a2 |
| 2-a | 1-a2 | a-2 | a2 |
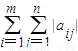 ,
,

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| 1 | 2 | 3 | -7 |
| -2 | 1 | 0 | 1 |
| a | a2-1 | -a | -a2 |
| 2-a | 1-a2 | a-2 | a2 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年北京市西城区高三(上)期末数学试卷(文科)(解析版) 题型:解答题
| a11 | a12 | … | a1n |
| a21 | a22 | … | a2n |
| • • • | • • • | … | • • • |
| an1 | an2 | … | ann |
 ri(A)+
ri(A)+ Cj(A).
Cj(A).| 1 | 1 | -1 | -1 |
| 1 | -1 | 1 | 1 |
| 1 | -1 | -1 | 1 |
| -1 | -1 | 1 | 1 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年北京市西城区高三(上)期末数学试卷(理科)(解析版) 题型:解答题
 (A)+
(A)+ (A)).
(A)).| a11 | a12 | … | a1n |
| a21 | a22 | … | a2n |
| … | … | … | … |
| an1 | an2 | … | ann |
查看答案和解析>>
科目:高中数学 来源:2012年北京市高考数学试卷(理科)(解析版) 题型:解答题
| 1 | 1 | -0.8 |
| 0.1 | -0.3 | -1 |
| 1 | 1 | c |
| a | b | -1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com