
已知函数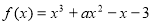 在
在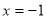 时取得极值.
时取得极值.
(1)求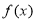 的解析式;
的解析式;
(2)求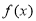 在区间
在区间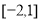 上的最大值.
上的最大值.
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:高中数学 来源: 题型:
| A、{-1,0,1,2} | B、{0,1,3} | C、{0,1,2} | D、{0,1} |
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修1-2 2.2结构图练习卷(解析版) 题型:选择题
如图是一个结构图,在□处应填入( )
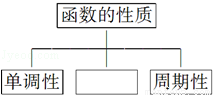
A.对称性 B.解析式 C.奇偶性 D.图象交换
查看答案和解析>>
科目:高中数学 来源:2014-2015学年甘肃省高二上学期第四次月考文科数学试卷(解析版) 题型:选择题
已知三棱锥的三视图如图所示,其中侧视图为直角三角形,俯视图为等腰直角三角形,则此三棱锥的体积等于

A.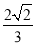 B .
B .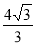 C.
C. 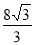 D.
D. 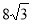
查看答案和解析>>
科目:高中数学 来源:[同步]2014年湘教版选修2-2 4.2导数的运算练习卷(解析版) 题型:?????
(2014•洛阳二模)已知任何一个三次函数f(x)=ax3+bx2+cx+d(a≠0)都有对称中心M(x0,f(x0)),记函数f(x)的导函数为f′(x),f′(x)的导函数为f″(x),则有f″(x)=0.若函数f(x)=x3﹣3x2,则f(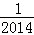 )+f(
)+f(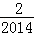 )+f(
)+f( )+…+f(
)+…+f(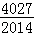 )=( )
)=( )
A.4027 B.﹣4027 C.8054 D.﹣8054
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com