
在底面边长为2,高为1的正四梭柱ABCD=A1B1C1D1中,E,F分别为BC,C1D1的中点.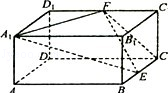
(1)求异面直线A1E,CF所成的角;
(2)求平面A1EF与平面ADD1A1所成锐二面角的余弦值.
(1)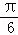 (2)
(2)
解析试题分析:(1)以D为原点建立空间直角坐标系,求出各点坐标,进而求出异面直线A1E,CF的方向向量,代入向量夹角公式,可得求异面直线A1E,CF所成的角;
(2)求平面A1EF与平面ADD1A1的法向量,代入向量夹角公式,可得二面角的余弦值.
以D为原点建立空间直角坐标系
(1)A1(2,0,1),E(1,2,0),C(0,2,0),F(0,1,1) ,
,
设异面直线A1E,CF所成的角为θ,则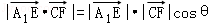 ,
,
即3= •
• •cosθ
•cosθ
解得cosθ=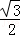
解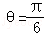 ,
,
所以,所求异面直线的夹角为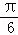
(2) ,设平面A1EF的法向量为
,设平面A1EF的法向量为 ,则
,则 ,
,
令x=1,则平面A1EF的一个法向量为 ,
,
平面ADD1A1的一个法向量为 ,
,
设平面A1EF与平面ADD1A1所成锐二面角为α,则
由 ,
,
即2= •1•cosα
•1•cosα
解得:
故平面A1EF与平面ADD1A1所成锐二面角的余弦值为
考点:用空间向量求平面间的夹角;用空间向量求直线间的夹角、距离
点评:本题考查的知识点是用空间向量求平面间的夹角,用空间向量求直线间的夹角,建立空间坐标系,将空间异面直线夹角问题及二面角问题转化为向量夹角问题是解答的关键.


科目:高中数学 来源: 题型:解答题
如图,在长方体AC1中,AB=BC=2, ,点E、F分别是面A1C1、面BC1的中心.
,点E、F分别是面A1C1、面BC1的中心.
(1)求证:BE//平面D1AC;
(2)求证:AF⊥BE;
(3)求异面直线AF与BD所成角的余弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E,E1,F分别是棱AD,AA1,AB的中点.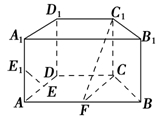
(1)证明:直线EE1∥平面FCC1;
(2)求二面角B-FC1-C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,四棱锥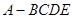 中,
中, 是正三角形,四边形
是正三角形,四边形 是矩形,且平面
是矩形,且平面 平面
平面 ,
, ,
, .
.
(Ⅰ)若点 是
是 的中点,求证:
的中点,求证: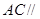 平面
平面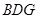 ;
;
(II)试问点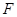 在线段
在线段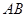 上什么位置时,二面角
上什么位置时,二面角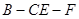 的余弦值为
的余弦值为 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知四棱锥P-ABCD的底面ABCD是边长为1的正方形,PD⊥底面ABCD,PD="AD." 
(Ⅰ)求证:BC∥平面PAD;
(Ⅱ)若E、F分别为PB,AD的中点,求证:EF⊥BC;
(Ⅲ)求二面角C-PA-D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,直三棱柱ABC—A1B1C1,底面△ABC中,CA=CB=1,∠BCA=90°,棱AA1=2,M、N分别是A1B1,A1A的中点;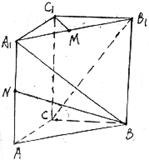
(1)求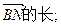
(2)求
(3)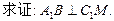
(4)求CB1与平面A1ABB1所成的角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com