
科目:高中数学 来源: 题型:
将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落,小球在下落过程中,将3次遇到黑色障碍物,最后落入A袋或B袋中。已知小球每次遇到黑色障碍物时向左、右两边下落的概率都是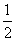 。
。
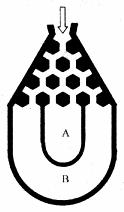
(1)求小球落入A袋中的概率P(A);
(2)在容器入口处依次放入4个小球,记X为落入A袋中小球的个数,试求X=3的概率和X的数学期望EX。
查看答案和解析>>
科目:高中数学 来源: 题型:
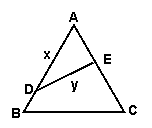
如图,公园有一块边长为2的等边△ABC的边角地,现修成草坪, 图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.
(1).设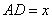 (x≥0),
(x≥0),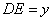 ,求用
,求用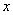 表示
表示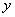 的函数关系
的函数关系
式,并求函数的定义域;
(2).如果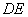 是灌溉水管,为节约成本,希望它最短,
是灌溉水管,为节约成本,希望它最短,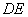 的
的
位置应在哪里?如果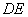 是参观线路,则希望它最长,
是参观线路,则希望它最长,
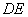 的位置又应在哪里?请予证明.
的位置又应在哪里?请予证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
)设函数
(1)写出函数f (x)的最小正周期及单调递增区间;
(2)当 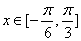 时,函数f (x)的最小值为2,求此时函数f (x)的最大值,并指出x取何值时函数f (x)取得最大值.
时,函数f (x)的最小值为2,求此时函数f (x)的最大值,并指出x取何值时函数f (x)取得最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
男运动员6名,女运动员4名,其中男女队长各1人,从中
选5人外出比赛,下列情形各有多少种选派方法
⑴男3名,女2名 ⑵队长至少有1人参加
⑶至少1名女运动员 ⑷既要有队长,又要有女运动员
查看答案和解析>>
科目:高中数学 来源: 题型:
某单位拟安排6位员工在今年5月1日至3日(劳动节假期)值班,每天安排2人,每人值班1天 . 若6位员工中的甲不值1日,乙不值2日,则不同的安排方法共有 种(用数字作答)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com