
【题目】2019年6月25日,《固体废物污染环境防治法(修订草案)》初次提请全国人大常委会审议,草案对“生活垃圾污染环境的防治”进行了专章规定.草案提出,国家推行生活垃圾分类制度.为了了解人民群众对垃圾分类的认识,某市环保部门对该市市民进行了一次垃圾分类网络知识问卷调查,每一位市民仅有一次参加机会,通过随机抽样,得到参加问卷调查的1000人的得分(满分:100分)数据,统计结果如表所示:
得分 |
|
|
|
|
|
|
|
频数 | 25 | 150 | 200 | 250 | 225 | 100 | 50 |
(1)由频数分布表可以认为,此次问卷调查的得分![]() 服从正态分布
服从正态分布![]() ,
,![]() 近似为这1000人得分的平均值(同一组数据用该组区间的中点值作为代表),请利用正态分布的知识求
近似为这1000人得分的平均值(同一组数据用该组区间的中点值作为代表),请利用正态分布的知识求![]() ;
;
(2)在(1)的条件下,市环保部门为此次参加问卷调查的市民制定如下奖励方案:
①得分不低于![]() “的可以获赠2次随机话费,得分低于
“的可以获赠2次随机话费,得分低于![]() 的可以获赠1次随机话费;
的可以获赠1次随机话费;
②每次获赠的随机话费和对应的概率为:
获赠的随机话费(单位:元) | 20 | 40 |
概率 |
|
|
现市民小王要参加此次问卷调查,记![]() (单位:元)为该市民参加问卷调查获赠的话费,求
(单位:元)为该市民参加问卷调查获赠的话费,求![]() 的分布列及数学期望.
的分布列及数学期望.
附:①![]() ;②若
;②若![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
科目:高中数学 来源: 题型:
【题目】已知直线![]() 过点
过点![]() ,倾斜角为
,倾斜角为![]() ,在以坐标原点为极点,
,在以坐标原点为极点,![]() 轴的非负半轴为极轴的极坐标系中,曲线
轴的非负半轴为极轴的极坐标系中,曲线![]() 的方程为
的方程为![]() .
.
(1)写出直线![]() 的参数方程和曲线
的参数方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,设点
两点,设点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥![]() 中,底面
中,底面![]() 是边长为6的正三角形,
是边长为6的正三角形,![]() 底面
底面![]() ,且
,且![]() 与底面
与底面![]() 所成的角为
所成的角为![]() .
.
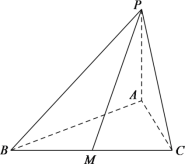
(1)求三棱锥![]() 的体积;
的体积;
(2)若![]() 是
是![]() 的中点,求异面直线
的中点,求异面直线![]() 与
与![]() 所成角的大小(结果用反三角函数值表示).
所成角的大小(结果用反三角函数值表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地要建造一个边长为2(单位:![]() )的正方形市民休闲公园
)的正方形市民休闲公园![]() ,将其中的区域
,将其中的区域![]() 开挖成一个池塘,如图建立平面直角坐标系后,点
开挖成一个池塘,如图建立平面直角坐标系后,点![]() 的坐标为
的坐标为![]() ,曲线
,曲线![]() 是函数
是函数![]() 图像的一部分,过边
图像的一部分,过边![]() 上一点
上一点![]() 在区域
在区域![]() 内作一次函数
内作一次函数![]() (
(![]() )的图像,与线段
)的图像,与线段![]() 交于点
交于点![]() (点
(点![]() 不与点
不与点![]() 重合),且线段
重合),且线段![]() 与曲线
与曲线![]() 有且只有一个公共点
有且只有一个公共点![]() ,四边形
,四边形![]() 为绿化风景区.
为绿化风景区.
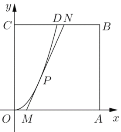
(1)求证:![]() ;
;
(2)设点![]() 的横坐标为
的横坐标为![]() ,
,
①用![]() 表示
表示![]() 、
、![]() 两点的坐标;
两点的坐标;
②将四边形![]() 的面积
的面积![]() 表示成关于
表示成关于![]() 的函数
的函数![]() ,并求
,并求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某贫困县在政府“精准扶贫”的政策指引下,充分利用自身资源,大力发展养茶业.该县农科所为了对比A,B两种不同品种茶叶的产量,在试验田上分别种植了A,B两种茶叶各![]() 亩,所得亩产数据(单位:千克)如下:
亩,所得亩产数据(单位:千克)如下:
A:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;
;
B:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;
;
(1)从A,B两种茶叶亩产数据中各任取1个,求这两个数据都不低于![]() 的概率;
的概率;
(2)从B品种茶叶的亩产数据中任取![]() 个,记这两个数据中不低于
个,记这两个数据中不低于![]() 的个数为
的个数为![]() ,求
,求![]() 的分布列及数学期望;
的分布列及数学期望;
(3)根据以上数据,你认为选择该县应种植茶叶A还是茶叶B?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业打算处理一批产品,这些产品每箱100件,以箱为单位销售.已知这批产品中每箱出现的废品率只有![]() 或者
或者![]() 两种可能,两种可能对应的概率均为0.5.假设该产品正品每件市场价格为100元,废品不值钱.现处理价格为每箱8400元,遇到废品不予更换.以一箱产品中正品的价格期望值作为决策依据.
两种可能,两种可能对应的概率均为0.5.假设该产品正品每件市场价格为100元,废品不值钱.现处理价格为每箱8400元,遇到废品不予更换.以一箱产品中正品的价格期望值作为决策依据.
(1)在不开箱检验的情况下,判断是否可以购买;
(2)现允许开箱,有放回地随机从一箱中抽取2件产品进行检验.
①若此箱出现的废品率为![]() ,记抽到的废品数为
,记抽到的废品数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
②若已发现在抽取检验的2件产品中,其中恰有一件是废品,判断是否可以购买.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校兴趣小组在如图所示的矩形区域![]() 内举行机器人拦截挑战赛,在
内举行机器人拦截挑战赛,在![]() 处按
处按![]() 方向释放机器人甲,同时在
方向释放机器人甲,同时在![]() 处按某方向释放机器人乙,设机器人乙在
处按某方向释放机器人乙,设机器人乙在![]() 处成功拦截机器人甲.若点
处成功拦截机器人甲.若点![]() 在矩形区域
在矩形区域![]() 内(包含边界),则挑战成功,否则挑战失败.已知
内(包含边界),则挑战成功,否则挑战失败.已知![]() 米,
米,![]() 为
为![]() 中点,机器人乙的速度是机器人甲的速度的2倍,比赛中两机器人均按匀速直线运动方式行进,记
中点,机器人乙的速度是机器人甲的速度的2倍,比赛中两机器人均按匀速直线运动方式行进,记![]() 与
与![]() 的夹角为
的夹角为![]() .
.
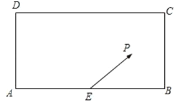
(1)若![]() ,
,![]() 足够长,则如何设置机器人乙的释放角度才能挑战成功?(结果精确到
足够长,则如何设置机器人乙的释放角度才能挑战成功?(结果精确到![]() );
);
(2)如何设计矩形区域![]() 的宽
的宽![]() 的长度,才能确保无论
的长度,才能确保无论![]() 的值为多少,总可以通过设置机器人乙的释放角度使机器人乙在矩形区域
的值为多少,总可以通过设置机器人乙的释放角度使机器人乙在矩形区域![]() 内成功拦截机器人甲?
内成功拦截机器人甲?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com