
����Ŀ��ij��Ҫ����һ���߳�Ϊ2����λ��![]() �����������������й�
�����������������й�![]() �������е�����
�������е�����![]() ���ڳ�һ����������ͼ����ƽ��ֱ������ϵ��
���ڳ�һ����������ͼ����ƽ��ֱ������ϵ��![]() ������Ϊ
������Ϊ![]() ������
������![]() �Ǻ���
�Ǻ���![]() ͼ���һ���֣�����
ͼ���һ���֣�����![]() ��һ��
��һ��![]() ������
������![]() ����һ�κ���
����һ�κ���![]() ��
��![]() ����ͼ�����߶�
����ͼ�����߶�![]() ���ڵ�
���ڵ�![]() ����
����![]() �����
�����![]() �غϣ������߶�
�غϣ������߶�![]() ������
������![]() ����ֻ��һ��������
����ֻ��һ��������![]() ���ı���
���ı���![]() Ϊ�̻��羰��.
Ϊ�̻��羰��.
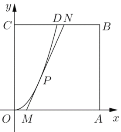
��1����֤��![]() ��
��
��2�����![]() �ĺ�����Ϊ
�ĺ�����Ϊ![]() ��
��
����![]() ��ʾ
��ʾ![]() ��
��![]() ��������ꣻ
��������ꣻ
�ڽ��ı���![]() �����
�����![]() ��ʾ�ɹ���
��ʾ�ɹ���![]() �ĺ���
���![]() ������
������![]() �����ֵ.
�����ֵ.
���𰸡���1����������2����M��![]() ��0����N��
��0����N��![]() ��2����S��4����t
��2����S��4����t![]() ��������0��t��1��S�����ֵ��4
��������0��t��1��S�����ֵ��4![]() ��
��
��������
��1�����ݺ���y��ax2����D���������ʽy��2x2��
��![]() ��ȥy����������0֤�����۳�����
��ȥy����������0֤�����۳�����
��2����д����P�����꣨t��2t2��������ֱ��MN�ķ��̣���t��ʾ��ֱ�߷��̣�
����ֱ�߷������M��N�����ꣻ
�ڽ��ı���MABN�����S��ʾ�ɹ���t�ĺ���S��t����
���û�������ʽ�������S�����ֵ��
��1������y��ax2����D��1��2����
��������a��2��
��y��2x2��
��![]() ����ȥy��2x2��kx��b��0��
����ȥy��2x2��kx��b��0��
���߶�MN������OD����ֻ��һ��������P��
����������k��2��4��2��b��0��
���b![]() ��
��
��2�����P�ĺ�����Ϊt����0��t��1��
���P��t��2t2����
��ֱ��MN�ķ���Ϊy��kx+b��
��y��kx![]() ����P��
����P��
��kt![]() 2t2��
2t2��
���k��4t��
y��4tx��2t2
��y��0�����x![]() ����M��
����M��![]() ��0����
��0����
��y��2�����x![]() ����N��
����N��![]() ��2����
��2����
�ڽ��ı���MABN�����S��ʾ�ɹ���t�ĺ���Ϊ
S��S��t����2��2![]() 2��[
2��[![]() ��
��![]() ��]��4����t
��]��4����t![]() ��������0��t��1��
��������0��t��1��
��t![]() 2
2![]() �����ҽ���t
�����ҽ���t![]() ����t
����t![]() ʱ������������
ʱ������������
����S��4![]() ����S�����ֵ��4
����S�����ֵ��4![]() ��
��


 �»����ܶ�Ա��ϵ�д�
�»����ܶ�Ա��ϵ�д� ����ͼ����ּ��������ҵ֣�ݴ�ѧ������ϵ�д�
����ͼ����ּ��������ҵ֣�ݴ�ѧ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �У�����
�У�����![]() Ϊ�����Σ�
������![]() ����
����![]() ��
��![]() ��
��![]() Ϊ�߶�
Ϊ�߶�![]() ���е㣮
���е㣮
��1����![]() Ϊ�߶�
Ϊ�߶�![]() �ϵĶ��㣬֤����ƽ��
�ϵĶ��㣬֤����ƽ��![]() ƽ��
ƽ��![]() ��
��
��2����![]() Ϊ�߶�
Ϊ�߶�![]() ��
��![]() ��
��![]() �ϵĶ��㣨����
�ϵĶ��㣨����![]() ��
��![]() ����
����![]() ������
������![]() ������Ƿ�������ֵ��������ڣ�������ֵ����������ڣ���˵�����ɣ�
������Ƿ�������ֵ��������ڣ�������ֵ����������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������![]() ������������
������������![]() ������
������![]() ������
������![]() ���������
���������![]() ������
Ϊ������![]() ���������У���Ϊ
���������У���Ϊ![]() .
.
��1���2018����������![]() ��
��
��2����֤��������������![]() ������Ψһ����������
������Ψһ����������![]() ��
��
��3������������![]() ��������ĺ�.
��������ĺ�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ��
��![]() �ֱ�Ϊ˫����
�ֱ�Ϊ˫����![]()
![]()
![]() �����ҽ��㣬��P����
�����ҽ��㣬��P����![]() Ϊֱ����Բ��C�ڵ�һ�����ڵĽ��㣬���߶�
Ϊֱ����Բ��C�ڵ�һ�����ڵĽ��㣬���߶�![]() ���е�Q��C�Ľ������ϣ���C�����������߷���Ϊ__________��
���е�Q��C�Ľ������ϣ���C�����������߷���Ϊ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ��
��![]() �ֱ�Ϊ˫����
�ֱ�Ϊ˫����![]()
![]()
![]() �����ҽ��㣬��P����
�����ҽ��㣬��P����![]() Ϊֱ����Բ��C�ڵ�һ�����ڵĽ��㣬���߶�
Ϊֱ����Բ��C�ڵ�һ�����ڵĽ��㣬���߶�![]() ���е�Q��C�Ľ������ϣ���C�����������߷���Ϊ__________��
���е�Q��C�Ľ������ϣ���C�����������߷���Ϊ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ƶ�֧������������������������������Ϊ�й��������Ĵ�����.Ϊ�˰���50�����ϵ��������˸������Ӧ���ƶ�֧����,ij����ͨ��������֯50�����ϵ���������ѧϰ�ƶ�֧�����֪ʶ.ѧϰ������,ÿ�˶�������ʱ���,�÷ֶ���![]() ��.����Щ���(�д������)��,������
��.����Щ���(�д������)��,������![]() ��,ͳ�Ƶ÷ֻ��Ƶ�ʷֲ�ֱ��ͼ��ͼ.
��,ͳ�Ƶ÷ֻ��Ƶ�ʷֲ�ֱ��ͼ��ͼ.
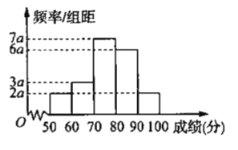
(1)���ͼ��![]() ��ֵ,����������,����ɼ���
��ֵ,����������,����ɼ���![]() �ϵ�����;
�ϵ�����;
(2)��������Ƶ��Ϊ����,�Ӳμ���δ������Ⱥ��,�����ȡ![]() ��,�dzɼ���
��,�dzɼ���![]() ������(��
������(��![]() ��)������Ϊ
��)������Ϊ![]() ,��
,��![]() �ķֲ��к�����.
�ķֲ��к�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ�����ͬ����С�� 5 ���ľ��һ�� 2 ����һ�� 3 ����Ҫ�ѻ�ľһ��һ���ȫ���ŵ�ij�������ÿ�� ֻ��ȡ������һ���������һ�飬��ͬ��ȡ����______�֣����������𣩣�
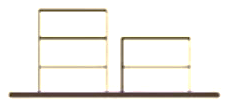
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
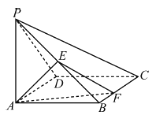
����Ŀ����ͼ��������P-ABCD�У�����ABCDΪƽ���ı��Σ���OΪ�Խ���BD���е㣬��E��F�ֱ�Ϊ��PC��PD���е㣬��֪PA��AB��PA��AD��
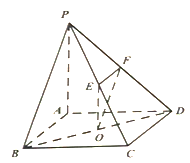
��1����֤��ֱ��PB��ƽ��OEF��
��2����֤��ƽ��OEF��ƽ��ABCD��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2016��1��6�գ��й�������ɹ����ϻ���ʽ�������й��ִ�ָ�����й��ִ�ָ���Ƿ�ӳ�ִ���ҵ��Ӫ�����г���Ҫ��Ʒ����״����仯���Ƶ�һ��ָ����ϵ����ͼ��ʾ������ͼ��2019�����ҵ������ҵ�IJִ�ָ���������.���ݸ�����ͼ�����н����в���ȷ���ǣ� ��
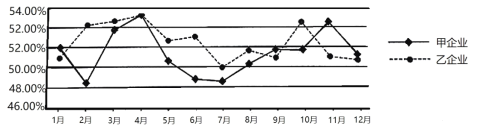
A.2019��1����4�¼���ҵ�IJִ�ָ��������ҵ�IJִ�ָ��������
B.����ҵ2019�����ƽ���ִ�ָ�����Ե�������ҵ2019�����ƽ���ִ�ָ��
C.����ҵ2019������ִ�ָ����������4�·�
D.2019��7����9������ҵ�IJִ�ָ�����������ڼ���ҵ
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com