
)定义在区间(-1,1)上的函数f(x)满足:对任意x,y∈(-1,1),都有f(x)+f(y)=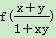 ,且当x∈(-1,0)时,有f(x)>0.
,且当x∈(-1,0)时,有f(x)>0.
(1)判定f(x)在区间(-1,1)上的奇偶性,并说明理由;
(2)判定f(x)在区间(-1,1)上的单调性,并给出证明;
(3)求证: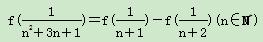 .
.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
抛掷一枚骰子,当它每次落地时,向上一面的点数称为该次抛掷的点数,可随机出现1到6点中的任一个结果.连续抛掷两次,第一次抛掷的点数记为a,第二次抛掷的点数记为b.
(1)求直线ax+by=0与直线x+2y+1=0平行的概率;
(2)求长度依次为a,b,2的三条线段能构成三角形的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
定义在R上的函数f(x)是偶函数,且f(x)=f(2-x).若f(x)在区间[1,2]上是减函数,则f(x)( )
A.在区间[-2,-1]上是增函数,在区间[3,4]上是增函数
B.在区间[-2,-1]上是增函数,在区间[3,4]上是减函数
C.在区间[-2,-1]上是减函数,在区间[3,4]上是增函数
D.在区间[-2,-1]上是减函数,在区间[3,4]上是减函数
查看答案和解析>>
科目:高中数学 来源: 题型:
设f(x)=kax-a-x(a>0且a≠1)是定义域为R的奇函数.
(1)若f(1)>0,求不等式f(x2+2x)+f(x-4)>0的解集;
(2)若f(1)=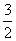 ,且g(x)=a2x+a-2x-4f(x),求g(x)在区间[1,+∞)上的最小值.
,且g(x)=a2x+a-2x-4f(x),求g(x)在区间[1,+∞)上的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)(x∈R)满足f(x+2)=f(x),且当x∈[-1,1]时,f(x)=1-|x|.若函数g(x)= 则函数h(x)=f(x)-g(x)在区间[-4,4]内的零点个数是________.
则函数h(x)=f(x)-g(x)在区间[-4,4]内的零点个数是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com