
在△ABC中,若0<tan A·tan B<1,那么 △ABC一定是( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.形状不确定
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题4第1课时练习卷(解析版) 题型:解答题
如图,四面体ABCD中,△ABC与△DBC都是边长为4的正三角形.

(1)求证:BC⊥AD;
(2)试问该四面体的体积是否存在最大值?若存在,求出这个最大值及此时棱长AD的大小;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题2第4课时练习卷(解析版) 题型:解答题
已知函数f(x)=2 sin(2ωx+φ)(ω>0,φ∈(0,π))的图象中相邻两条对称轴间的距离为
sin(2ωx+φ)(ω>0,φ∈(0,π))的图象中相邻两条对称轴间的距离为 ,且点
,且点 是它的一个对称中心.
是它的一个对称中心.
(1)求f(x)的表达式;
(2)若f(ax)(a>0)在 上是单调递减函数,求a的最大值.
上是单调递减函数,求a的最大值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题2第3课时练习卷(解析版) 题型:选择题
已知 =1-yi,其中x,y是实数,i是虚数单位,则x+yi的共轭复数为( )
=1-yi,其中x,y是实数,i是虚数单位,则x+yi的共轭复数为( )
A.1+2i B.1-2i C.2+i D.2-i
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题2第2课时练习卷(解析版) 题型:填空题
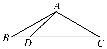
如图,在△ABC中,已知点D在BC边上,AD⊥AC,sin∠BAC=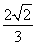 ,AB=3
,AB=3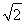 ,AD=3,则BD的长为________.
,AD=3,则BD的长为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题2第1课时练习卷(解析版) 题型:解答题
函数f(x)=Asin  +1(A>0,ω>0)的最大值为3,其图象相邻两条对称轴之间的距离为
+1(A>0,ω>0)的最大值为3,其图象相邻两条对称轴之间的距离为 .
.
(1)求函数f(x)的解析式;
(2)设α∈ ,f
,f  =2,求α的值.
=2,求α的值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题2第1课时练习卷(解析版) 题型:选择题
设函数f(x)=sin  +sin
+sin  (ω>0)的最小正周期为π,则( )
(ω>0)的最小正周期为π,则( )
A.f(x)在 上单调递减 B.f(x)在
上单调递减 B.f(x)在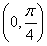 上单调递增
上单调递增
C.f(x)在 上单调递增 D.f(x)在
上单调递增 D.f(x)在 上单调递减
上单调递减
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题1第5课时练习卷(解析版) 题型:选择题
已知e为自然对数的底数,则函数y=xex的单调递增区间是( )
A.[-1,+∞) B.(-∞,-1]
C.[1,+∞) D.(-∞,1]
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题1第1课时练习卷(解析版) 题型:填空题
设命题p:?a>0,a≠1,函数f(x)=ax-x-a有零点.则?p: ________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com